Question

17．如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别是R、S，若AQ=PQ，PR=PS，下面五个结论：①AS=AR；②PQ∥AR；③∠SPC+∠BPR=∠PQC；④S_{四边形ARPQ}=$\frac{1}{2}$S_△ABC；⑤BR+CS=SQ．其中正确的结论有（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 连接AP，△APR≌△APS，可得AS=AR；∠PQC=∠APQ+∠QAP=2∠QAP=∠PAB+∠PAQ=∠BAQ，则PQ∥AB；∠SPC+∠BPR=90°-∠C+90°-∠B=180°-（∠B+∠C）=∠BAC=∠PQC；依此判断①②③正确；根据已知条件不能得出④⑤正确．

解答 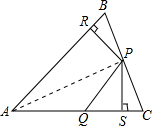解：连接AP，
在△APR和△APS中，
∵∠ARP=∠ASP=90°，
∴在Rt△APR和Rt△APS中，
∵$\left\{\begin{array}{l}{AP=AP}\\{PR=PS}\end{array}\right.$，
∴△APR≌△APS（HL），
∴AS=AR，故①正确；
∠BAP=∠SAP，
∴∠SAB=∠BAP+∠SAP=2∠SAP，
在△AQP中，
∵AQ=PQ，
∴∠QAP=∠APQ，
∴∠CQP=∠QAP+∠APQ=2∠QAP=2∠SAP．
∴PQ∥AB，故②正确；
∵∠SPC=90°-∠C，∠BPR=90°-∠B，
∴∠SPC+∠BPR=90°-∠C+90°-∠B=180°-（∠B+∠C）=∠BAC，
∵PQ∥AB，
∴∠BAC=∠PQC，
∴∠SPC+∠BPR=∠PQC，故③正确；
∵S_{四边形ARPQ}=S_△APR+S_△APQ=$\frac{1}{2}$AR•PR+$\frac{1}{2}$AQ•PS=$\frac{1}{2}$PR（AR+AQ），
S_△ABC=S_△APB+S_△APC=$\frac{1}{2}$AB•PR+$\frac{1}{2}$AC•PS=$\frac{1}{2}$PR（AB+AC），
根据已知条件不能得出AR+AQ=$\frac{1}{2}$（AB+AC），故④错误；
根据已知条件不能得出BR+CS=SQ，故⑤错误．
故选C．

点评 此题考查了角平分线的性质及全等三角形的判定和平行线的判定定理；正确作出辅助线是解答本题的关键．