
分析 根据顶点在线段AB上抛物线与y轴的交点坐标为(0,c)可以判断出c的取值范围,得到①错误;根据二次函数的增减性判断出②正确;先确定x=1时,点D的横坐标取得最大值,然后根据二次函数的对称性求出此时点C的横坐标,即可判断③错误;令y=0,利用根与系数的关系与顶点的纵坐标求出CD的长度的表达式,然后根据平行四边形的对边平行且相等可得AB=CD,然后列出方程求出a的值,判断出④正确,可得出答案.
解答 解:∵点A,B的坐标分别为(-2,3)和(1,3),
∴线段AB与y轴的交点坐标为(0,3),
又∵抛物线的顶点在线段AB上运动,抛物线与y轴的交点坐标为(0,c),
∴c≤3,(顶点在y轴上时取“=”),故①错误;
∵抛物线的顶点在线段AB上运动,
∴当x<-2时,y随x的增大而增大,
因此,当x<-3时,y随x的增大而增大,故②正确;
若点D的横坐标最大值为5,则此时对称轴为直线x=1,
根据二次函数的对称性,点C的横坐标最小值为-2-4=-6,故③错误;
根据顶点坐标公式,$\frac{4ac-{b}^{2}}{4a}$=3,
令y=0,则ax2+bx+c=0,
CD2=(-$\frac{b}{a}$)2-4×$\frac{c}{a}$=$\frac{{b}^{2}-4ac}{{a}^{2}}$,
根据顶点坐标公式,$\frac{4ac-{b}^{2}}{4a}$=3,
∴$\frac{{b}^{2}-4ac}{a}$=-12,
∴CD2=$\frac{1}{a}$×(-12)=$\frac{12}{-a}$,
∵四边形ACDB为平行四边形,
∴CD=AB=1-(-2)=3,
∴$\frac{12}{-a}$=32=9,
解得a=-$\frac{4}{3}$,故④正确;
综上所述,正确的结论有②④.
故答案为:②④.
点评 本题考查了二次函数的综合题型,主要利用了二次函数的顶点坐标,二次函数的对称性,根与系数的关系,平行四边形的对边平行且相等的性质.在判断①要注意顶点在y轴上的情况.本题知识点较多,综合性较强,有一定的难度,容易出现错误.


科目:初中数学 来源: 题型:解答题
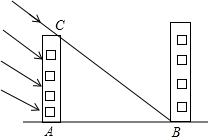 冬至是一年时间中太阳相对地球北半球位置最低的一天,只要这一天采到阳光,一年四季均能受到阳光的照射,此时竖立一根1米长的竹竿,其影长为1.5米,某单位计划建30米高的南北两栋办公楼,如图所示,问两楼相距多少米时,后楼的采光刚好一年四季都不受影响?
冬至是一年时间中太阳相对地球北半球位置最低的一天,只要这一天采到阳光,一年四季均能受到阳光的照射,此时竖立一根1米长的竹竿,其影长为1.5米,某单位计划建30米高的南北两栋办公楼,如图所示,问两楼相距多少米时,后楼的采光刚好一年四季都不受影响?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 摸到2个白球 | B. | 摸到2个黑球 | ||
| C. | 摸到1个白球,1个黑球 | D. | 摸到1个黑球,1个红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面五个结论:①AS=AR;②PQ∥AR;③∠SPC+∠BPR=∠PQC;④S四边形ARPQ=$\frac{1}{2}$S△ABC;⑤BR+CS=SQ.其中正确的结论有( )
如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面五个结论:①AS=AR;②PQ∥AR;③∠SPC+∠BPR=∠PQC;④S四边形ARPQ=$\frac{1}{2}$S△ABC;⑤BR+CS=SQ.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com