
【题目】将一副直角三角板如图1,摆放在直线![]() 上(直角三角板
上(直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板
,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 以每秒5°的速度顺时针旋转,旋转时间为t秒.当
以每秒5°的速度顺时针旋转,旋转时间为t秒.当![]() 与射线
与射线![]() 意合时停止旋转.
意合时停止旋转.
(1)如图2.当![]() 为
为![]() 的角平分线时,求此时
的角平分线时,求此时![]() 的值?
的值?
(2)当![]() 旋转至
旋转至![]() 的内部时,求
的内部时,求![]() 与
与![]() 的数量关系?
的数量关系?
(3)在旋转过程中,当三角板![]() 的其中一边平行于三角板
的其中一边平行于三角板![]() 的某一边时,求此时
的某一边时,求此时![]() 等于______.(直接写出答案即可)
等于______.(直接写出答案即可)

【答案】(1)3s(2)∠ECB∠DCA=15°(3)15s或24s或27s或33s
【解析】
(1)先计算∠DCE的度数,再根据角平分线的定义和旋转的速度可得t的值;
(2)分别表示∠DCA与∠ECB的度数,相减可得数量关系;
(3)分五种情况讨论:AB分别和△DCE三边平行,还有AC∥DE,计算旋转角并根据速度列方程可得结论.
(1)如图2,∵∠EDC=90°,∠DEC=60°,
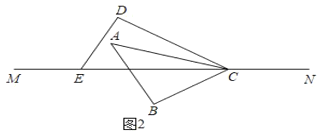
∴∠DCE=30°,
∵AC平分∠DCE,
∴∠ACE=![]() ∠DCE=15°,
∠DCE=15°,
∴t=![]() =3,
=3,
答:此时t的值是3s;
(2)当AC旋转至∠DCE的内部时,如图3,∠DCA与∠ECB的数量关系是:∠ECB∠DCA=15°;
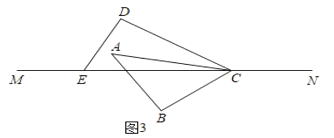
理由是:由旋转得:∠ACE=5t,
∴∠DCA=30°5t,∠ECB=45°5t,
∴∠ECB∠DCA=(45°5t)(30°5t)=15°;
(3)分四种情况:
①当AB∥DE时,如图4,∠ACE=45°+30°=5°t,
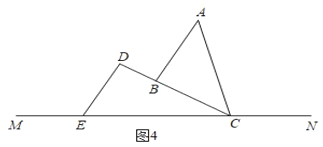
t=15;
②当AB∥CE时,如图5,则∠BCE=∠B=90°,
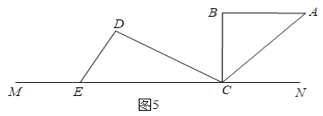
∴∠ACE=90°+45°=5°t,
t=27;
③当AB∥CD时,如图6,则∠DCB=∠B=90°,
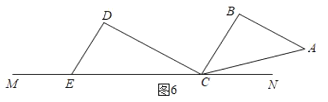
∠ACE=30°+90°+45°=5°t,
t=33;
④当AC∥DE时,如图7,
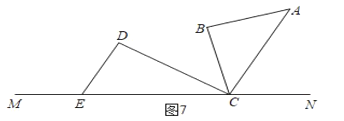
∴∠ACD=∠D=90°,
∴∠ACE=90°+30°=5°t,
t=24;
⑤当BC∥DE时,90°+30°+45°=5°t
∴t=33
综上,t的值是15s或24s或27s或33s.
故答案为:15s或24s或27s或33s.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2﹣3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 .
(2)将跳绳次数在160~190的选手依次记为A1、A2、…An,从中随机抽取两名选手作经验交流,请用树状或列表法求恰好抽取到的选手A1和A2的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汶川地震发生后,全国人民抗震救灾,众志成城某地政府急灾民之所需,立即组织![]() 辆汽车,将
辆汽车,将![]() 三种救灾物资共
三种救灾物资共![]() 吨一次性运往灾区,假设甲、乙,丙三种车型分别运载
吨一次性运往灾区,假设甲、乙,丙三种车型分别运载![]() 三种物资,根据下表提供的信息解答下列问题:
三种物资,根据下表提供的信息解答下列问题:
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
(1)设装运![]() 品种物资的车辆数分别为
品种物资的车辆数分别为![]() 试用含
试用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)据(1)中的表达式,试求![]() 三种物资各几吨.
三种物资各几吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )

A.4cm2 B.6cm2 C.8cm2 D.9cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE⊥BC,交BC于点E.
(1)求证:DE是⊙O的切线;
(2)如果CD=8,CE=6,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动,某读书小组随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、文艺类、科普类、其他等四类),并将调查结果绘制成如图所示的两幅不完整的统计图,请你结合图中的信息解答下列问题
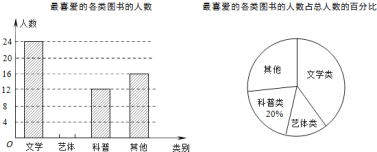
(1)被调查的学生人数为 人;
(2)科普类圆心角度数为 度,补全条形统计图;
(3)已知该校有1800名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
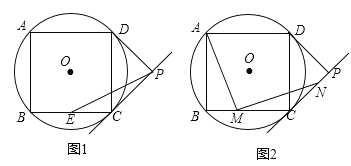
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AEM+∠CDN=180°,EC平分∠AEF.

(1)若∠EFC=62°,求∠C的度数;
(2)若CE⊥MN,垂足为点E,求证:∠FDE=∠FED.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com