
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.

【答案】(1)![]() ;(2)Q(4,1)或Q(1+
;(2)Q(4,1)或Q(1+![]() ,2
,2![]() ﹣2).
﹣2).
【解析】试题分析:(1)根据已知条件易求P点的坐标,把P点的坐标代入y=![]() ,即可求得k值,从而求得双曲线的解析式;(2)设Q点坐标为(a,b),根据Q点在双曲线上求得a、b之间的关系,再求得BO、AO的长,分△QCH∽△BAO和△QCH∽△ABO两种情况求Q点的坐标.
,即可求得k值,从而求得双曲线的解析式;(2)设Q点坐标为(a,b),根据Q点在双曲线上求得a、b之间的关系,再求得BO、AO的长,分△QCH∽△BAO和△QCH∽△ABO两种情况求Q点的坐标.
试题解析:
(1)把A(-2,0)代入y=ax+1中求得a=![]() ,所以y=
,所以y=![]() x+1,求得P点坐标为(2,2).
x+1,求得P点坐标为(2,2).
把P(2,2)代入y=![]() 求得k=4,所以双曲线的解析式为y=
求得k=4,所以双曲线的解析式为y=![]() .
.
(2)设Q点坐标为(a,b).
因为Q(a,b)在y=![]() 上,所以b=
上,所以b=![]() .由y=
.由y=![]() x+1,可得B点坐标为(0,1),则BO=1.由A点坐标为(-2,0),得AO=2.
x+1,可得B点坐标为(0,1),则BO=1.由A点坐标为(-2,0),得AO=2.
当△QCH∽△BAO时,![]() =
=![]() ,即
,即![]() =
=![]() ,所以a-2=2b,a-2=2×
,所以a-2=2b,a-2=2×![]() ,解得a=4或a=-2(舍去),所以Q点坐标为(4,1).
,解得a=4或a=-2(舍去),所以Q点坐标为(4,1).
当△QCH∽△ABO时,![]() =
=![]() ,即
,即![]() =
=![]() ,所以2a-4=
,所以2a-4=![]() ,解得a=1+
,解得a=1+![]() 或a=1-
或a=1-![]() (舍去),所以Q点坐标为(1+
(舍去),所以Q点坐标为(1+![]() ,2
,2![]() -2).
-2).
综上所述,Q点坐标为(4,1)或(1+![]() ,2
,2![]() -2).
-2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为![]() .
.
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
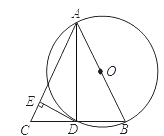
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O半径为5,∠BAC=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
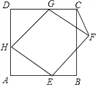
【题目】已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.
(1)当DG=2时,求△FCG的面积;
(2)设DG=x,用含x的代数式表示△FCG的面积;
(3)判断△FCG的面积能否等于1,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,4张如图1的长为a,宽为b(a>b)长方形纸片,按图2的方式放置,阴影部分的面积为S1,空白部分的面积为S2,若S2=2S1,则a,b满足( )
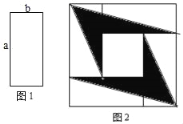
A. a=![]() B. a=2bC. a=
B. a=2bC. a=![]() bD. a=3b
bD. a=3b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,①检测深圳的空气质量; ②为了解某中东呼吸综合征(MERS)确诊病人同一架飞机乘客的健康情况;③为保证“神舟9号”成功发射,对其零部件进行检查;④调查某班50名同学的视力情况。其中适合采用抽样调查的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com