Question

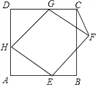
【题目】已知，如图，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD边AB，CD，DA上，AH=2，连接CF．

（1）当DG=2时，求△FCG的面积；

（2）设DG=x，用含x的代数式表示△FCG的面积；

（3）判断△FCG的面积能否等于1，并说明理由．

Answer 1

【答案】(1)4;(2)6-x;(3)见解析.

【解析】分析：(1)要求△FCG的面积,可以转化到面积易求的三角形中,通过证明△DGH≌△CFG得出.(2)欲求△FCG的面积,由已知得CG的长易求,只需求出GC边的高,通过证明△AHE≌△MFG可得;
(3)若 ,由,得x=5,此时,在△DGFH中,HG=.相应地,在△AHE中,AE=>6,即点E已经不在边AB上.故不可能有.

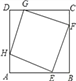
详解：（1）∵正方形ABCD中，AH=2，

∴DH=4，

∵DG=2，

∴HG=2，即菱形EFGH的边长为2．

在△AHE和△DGH中，

∵∠A=∠D=90°，AH=DG=2，EH=HG=2，

∴△AHE≌△DGH（HL），

∴∠AHE=∠DGH，

∵∠DGH+∠DHG=90°，

∴∠DHG+∠AHE=90°，

∴∠GHE=90°，即菱形EFGH是正方形，

同理可以证明△DGH≌△CFG，

∴∠FCG=90°，即点F在BC边上，同时可得CF=2，

从而S△FCG=×4×2=4．

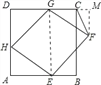
（2）作FM⊥DC，M为垂足，连接GE，

∵AB∥CD，

∴∠AEG=∠MGE，

∵HE∥GF，

∴∠HEG=∠FGE，

∴∠AEH=∠MGF．

在△AHE和△MFG中，

∴△AHE≌△MFG（AAS），

∴FM=HA=2，

即无论菱形EFGH如何变化，点F到直线CD的距离始终为定值2．

因此S△FCG=×2×（6﹣x）=6﹣x．

（3）若S△FCG=1，由（2）知S△FCG=6﹣x，得x=5，

∴在△DGH中，HG=，

∴在△AHE中，AE=，即点E已经不在边AB上．

∴不可能有S△FCG=1．

另法：∵点G在边DC上，

∴菱形的边长至少为DH=4，

当菱形的边长为4时：

∵点E在AB边上且满足AE=2，此时，当点E逐渐向右运动至点B时，HE的长（即菱形的边长）将逐渐变大，

∴最大值为HE=2．

此时，DG=2，故0≤x≤2．

∵函数S△FCG=6﹣x的值随着x的增大而减小，

∴当x=2时，S△FCG取得最小值为6﹣2．

又∵6﹣2=1，

∴△FCG的面积不可能等于1．