
【题目】如图,菱形![]() 中,
中,![]() 于
于![]() ,交
,交![]() 于F,
于F,![]() 于
于![]() ,若
,若![]() 的周长为4,则菱形
的周长为4,则菱形![]() 的面积为( ).
的面积为( ).

A.![]() B.
B.![]() C.16D.
C.16D.![]()
【答案】B
【解析】
由菱形的性质得到∠BCD=45°,推出△BFG与△BEC是等腰直角三角形,根据全等三角形的性质得到FG=FE,CG=CE,设BG=FG=EF=x,得到BF=![]() x,根据△BFG的周长为4,列方程x+x+
x,根据△BFG的周长为4,列方程x+x+![]() x=4,即可得到结论.
x=4,即可得到结论.
∵菱形ABCD中,∠D=135°,
∴∠BCD=45°,
∵BE⊥CD于E,FG⊥BC于G,
∴△BFG与△BEC是等腰直角三角形,
∵∠GCF=∠ECF,∠CGF=∠CEF=90°,
CF=CF,
∴△CGF≌△CEF(AAS),
∴FG=FE,CG=CE,
设BG=FG=EF=x,
∴BF=![]() x,
x,
∵△BFG的周长为4,
∴x+x+![]() x=4,
x=4,
∴x=4-2![]() ,
,
∴BE=2![]() ,
,
∴BC=![]() BE=4,
BE=4,
∴菱形ABCD的面积=4×2![]() =8
=8![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动.将大小不相同的正方形ABCD与正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG=BE且DG⊥BE,请你给出证明;
(2)如图2,小明将正方形ABCD绕点A转动,当点B恰好落在线段DG上时
①猜想线段DG和BE的位置关系是 .
②若AD=2![]() ,AE=
,AE=![]() ,求△ADG的面积.
,求△ADG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y=![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
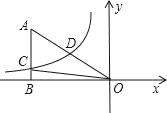
A. 12 B. 9 C. 6 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,9……,排成如图的数表:

(1)十字框的5个数的和与中间的数23有什么关系,若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗.
(2)设十字框中中间的数为![]() ,用含
,用含![]() 的式子表示十字框中的5个数之和.
的式子表示十字框中的5个数之和.
(3)十字框中的5个数的和能等于1045吗.若能,请写出这5个数,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{﹣3,2}=2.
(1)max{![]() ,3}= ;
,3}= ;
(2)已知y1=![]() 和y2=k2x+b在同一坐标系中的图象如图所示,若max{
和y2=k2x+b在同一坐标系中的图象如图所示,若max{![]() ,k2x+b}=
,k2x+b}=![]() ,结合图象,直接写出x的取值范围;
,结合图象,直接写出x的取值范围;
(3)用分类讨论的方法,求max{2x+1,x﹣2}的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com