
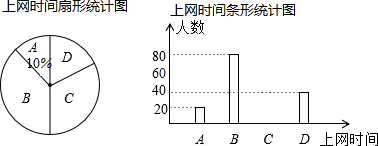
分析 (1)根据上网时间为A的人数和所占的百分比即可求出总人数;
(2)用总人数减去A、B和D类的人数,求出C类的人数,从而补全统计图;
(3)用全校的总人数乘以每周上网不超过7小时的学生人数所占的百分比,即可求出答案.
解答 解(1)参加调查的学生有$\frac{20}{10%}$=200(人),
故答案为:200;
(2)上网时间为C的人数是:200-20-80-40=60(人),
补图如图所示:
(3)根据题意得:
3600×$\frac{20+80+60}{200}$=2880(人),
答:全校上网不超过7小时的学生人数是2880人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 笔记本(本) | 20 | 15 |
| 钢笔(支) | 12 | 25 |
| 总价(元) | 312 | 330 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
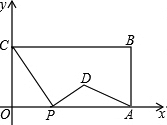 如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=6,OC=4.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则
如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=6,OC=4.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
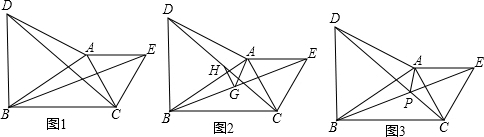
 如图,EF∥AD,∠1=∠2,∠BAC=87°,将求∠AGD的过程填写完整.
如图,EF∥AD,∠1=∠2,∠BAC=87°,将求∠AGD的过程填写完整.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com