
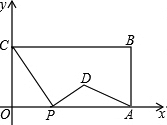
 如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=6,OC=4.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则
如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=6,OC=4.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 过点D作DH⊥OA于H,易证△COP∽△PHD,从而可得PH=2,HD=$\frac{t}{2}$,由此可确定命题(1)、(2)、(3)的真假,然后设点D的坐标为(x,y),则有$\left\{\begin{array}{l}{x=t+2}\\{y=\frac{t}{2}}\end{array}\right.$,消去t,即可得到点D始终在直线y=$\frac{1}{2}$(x-2)上,然后只需找出点D的始点和终点,再运用两点间距离公式即可算出点D运动路线的长.
解答 解: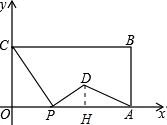 过点D作DH⊥OA于H,如图,
过点D作DH⊥OA于H,如图,
则有∠DHP=90°.
∵∠COP=∠CPD=90°,
∴∠COP=∠DHP,∠OCP=∠DPH=90°-∠OPC,
∴△COP∽△PHD,
∴$\frac{CO}{PH}$=$\frac{OP}{HD}$=$\frac{CP}{PD}$=2.
∵OC=4,OP=t,
∴PH=2,HD=$\frac{t}{2}$,
∴OH=t+2,
∴点D的坐标为(t+2,$\frac{1}{2}$t).
∴(1)正确.
当t=3时,PA=6-3=3,DH=$\frac{3}{2}$,
则△DPA的面积=$\frac{1}{2}$PA•DH=$\frac{1}{2}$×3×$\frac{3}{2}$=$\frac{9}{4}$.
∴(2)正确.
当t=4时,OH=t+2=6,此时点D在线段AB上,△DPA为直角三角形.
∴(3)错误.
设点D的坐标为(x,y),
则有$\left\{\begin{array}{l}{x=t+2}\\{y=\frac{t}{2}}\end{array}\right.$,
消去t,得y=$\frac{1}{2}$(x-2),
∴点D在直线y=$\frac{1}{2}$(x-2)上运动.
当t=0时,点D的坐标为(2,0);
当t=6时,点D的坐标为(8,3);
根据两点间距离公式可得:
点D运动路线的长为$\sqrt{(8-2)^{2}+(3-0)^{2}}$=3$\sqrt{5}$.
∴(4)错误.
故选B.
点评 本题是一道选择题,用到了相似三角形的判定与性质、两点间距离公式,要说明一个命题是假命题只需举一个反例即可,运用消元法得到点D在直线上运动是解决第(4)小题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:填空题
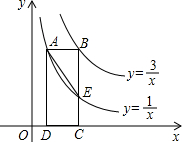 如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.
如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
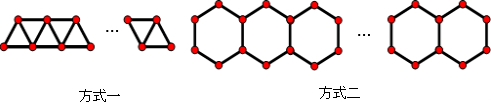
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
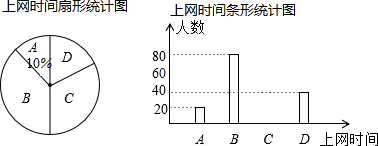
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
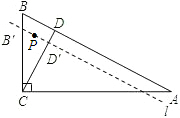 如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
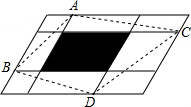 如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为100cm2,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形ABDC的面积是60cm2.
如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为100cm2,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形ABDC的面积是60cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com