
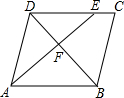
 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )| A. | 3:4 | B. | 9:16 | C. | 4:9 | D. | 1:3 |
分析 设DE=3k,EC=k,则CD=4k,由四边形ABCD是平行四边形,推出AB=CD=4k,DE∥AB,推出△DEF∽△BAF,推出$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{DE}{AB}$)2由此即可解决问题.
解答  解:设DE=3k,EC=k,则CD=4k,
解:设DE=3k,EC=k,则CD=4k,
∵四边形ABCD是平行四边形,
∴AB=CD=4k,DE∥AB,
∴△DEF∽△BAF,
∴$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{DE}{AB}$)2=($\frac{3k}{4k}$)2=$\frac{9}{16}$,
故选B.
点评 本题考查相似三角形的性质和判定、平行四边形的性质等知识,解题的关键是灵活运用平行四边形的性质,学会利用参数解决问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
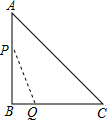 如图,在△ABC中,∠B=90°,AB=BC=4,动点P从点A出发沿A→B→C运动,动点Q从点B出发沿B→C→A运动.如果P、Q两点同时出发,速度均为1个单位/秒.设出发时间为x秒(0≤x≤8),记△PBQ的面积y1的函数图象为T.若直线y2=x+b与T只有一个交点,则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$.
如图,在△ABC中,∠B=90°,AB=BC=4,动点P从点A出发沿A→B→C运动,动点Q从点B出发沿B→C→A运动.如果P、Q两点同时出发,速度均为1个单位/秒.设出发时间为x秒(0≤x≤8),记△PBQ的面积y1的函数图象为T.若直线y2=x+b与T只有一个交点,则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )| A. | 2π-4 | B. | 4π-8 | C. | 2π-8 | D. | 4π-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
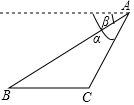 地震后,全国各地纷纷捐款捐物,一架满载救援物资的飞机到达灾区的上空时,为了能准确空投救援物资,在A处测得空投动点C的俯角α=60°,测得地面指挥台的俯角β=30°,如果B、C两地间的距离是2000米,则此时飞机距地面的高度是多少米?(结果保留根号)
地震后,全国各地纷纷捐款捐物,一架满载救援物资的飞机到达灾区的上空时,为了能准确空投救援物资,在A处测得空投动点C的俯角α=60°,测得地面指挥台的俯角β=30°,如果B、C两地间的距离是2000米,则此时飞机距地面的高度是多少米?(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com