
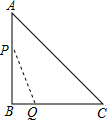
 如图,在△ABC中,∠B=90°,AB=BC=4,动点P从点A出发沿A→B→C运动,动点Q从点B出发沿B→C→A运动.如果P、Q两点同时出发,速度均为1个单位/秒.设出发时间为x秒(0≤x≤8),记△PBQ的面积y1的函数图象为T.若直线y2=x+b与T只有一个交点,则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$.
如图,在△ABC中,∠B=90°,AB=BC=4,动点P从点A出发沿A→B→C运动,动点Q从点B出发沿B→C→A运动.如果P、Q两点同时出发,速度均为1个单位/秒.设出发时间为x秒(0≤x≤8),记△PBQ的面积y1的函数图象为T.若直线y2=x+b与T只有一个交点,则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$. 分析 分0≤x≤4和4<x≤8两种情况,利用三角形的面积公式找出y1关于x函数关系式,依此画出图象T,再逐一分析直线y2=x+b与T相切或过(0,0)、(8,4$\sqrt{2}$)时b的值,结合图形即可得出结论.
解答 解:当0≤x≤4时,y1=$\frac{1}{2}$PB•BQ=$\frac{1}{2}$(4-x)x=-$\frac{1}{2}$x2+2x;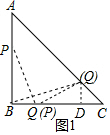
当4<x≤8时,过点Q作QD⊥BC与点D,如图1所示,
∵在△ABC中,∠B=90°,AB=BC=4,
∴∠ACB=45°,
∴QD=CQ•sin∠ACB=$\frac{\sqrt{2}}{2}$(x-4),
∴y1=$\frac{1}{2}$BP•QD=$\frac{1}{2}$(x-4)•$\frac{\sqrt{2}}{2}$(x-4)=$\frac{\sqrt{2}}{4}$(x-4)2.
画出函数图象T,如图2所示.
当直线y2=x+b与y1=-$\frac{1}{2}$x2+2x(0≤x≤4)相切时,将y2=x+b代入y1=-$\frac{1}{2}$x2+2x中,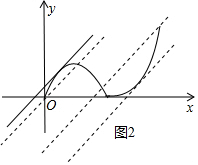
整理得:-$\frac{1}{2}$x2+x-b=0,
∵△=12-4×(-$\frac{1}{2}$)×(-b)=0,
∴b=$\frac{1}{2}$;
当直线y2=x+b过点(0,0)时,有0=b;
当直线y2=x+b过点(8,4$\sqrt{2}$)时,有4$\sqrt{2}$=8+b,
解得:b=4$\sqrt{2}$-8;
当直线y2=x+b与y1=$\frac{\sqrt{2}}{4}$(x-4)2(4<x≤8)相切时,将y2=x+b代入y1=$\frac{\sqrt{2}}{4}$(x-4)2中,
整理得:$\sqrt{2}$x2-(8$\sqrt{2}$+4)x+16-4b=0,
∵△=$[-(8\sqrt{2}+4)]^{2}$-4×$\sqrt{2}$×(16-4b)=0,
∴b=-$\frac{9\sqrt{2}}{2}$.
综上所述:当直线y2=x+b与T只有一个交点,b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$.
故答案为:b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$.
点评 本题考查了动点问题的函数图象、三角形的面积、根的判别式以及一次函数图象上点的坐标特征,依照题意画出图象T,利用数形结合解决问题是解题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
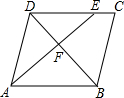 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )| A. | 3:4 | B. | 9:16 | C. | 4:9 | D. | 1:3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com