
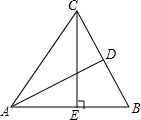
 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=50°,∠BCE=30°,求∠ADB的度数.
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=50°,∠BCE=30°,求∠ADB的度数. 分析 根据AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,可得∠BAD和∠CAD相等,都为30°,∠CEA=90°,从而求得∠ACE的度数,又因为∠BCE=40°,∠ADB=∠BDE+∠ACE+∠CAD,从而求得∠ADB的度数.
解答 解:∵AD是△ABC的角平分线,CE是△ABC的高,∠BAC=50°.
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=25°,∠CEA=90°.
∵∠CEA+∠BAC+∠ACE=180°.
∴∠ACE=40°.
∵∠ADB=∠BCE+∠ACE+∠CAD,∠BCE=30°.
∴∠ADB=40°+30°+35°=95°.
点评 本题考查三角形的内角和、角的平分线、三角形的一个外角等于和它不相邻的内角的和,关键是根据具体目中的信息,灵活变化,求出相应的问题的答案


科目:初中数学 来源: 题型:选择题
| A. | 系数是a,次数是6 | B. | 没有系数,次数是7 | ||
| C. | 系数是1,次数是6 | D. | 系数是1,次数是7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a-\frac{1}{3}=b-\frac{1}{3}$ | B. | $-\frac{3}{4}a=-\frac{3}{4}b$ | C. | 3a-1=3b-1 | D. | $\frac{a}{c}=\frac{b}{c}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com