解:(1)∵抛物线y=ax
2-2ax-3a,
∴当x=0时,y=-3a,
∴与y轴交点A的坐标为(0,-3a).
∵抛物线y=ax
2-2ax-3a交x轴于B,C两点(B在C右边),
∴a≠0,
令y=0,解得x=3或-1,
∴B(3,0),C(-1,0),
又∵y=ax
2-2ax-3a=a(x-1)
2-4a,
∴顶点D的坐标为(1,-4a);
(2)由(1)知A(0,-3a),D(1,-4a),
∴AD
2=1+(-3a+4a)
2=1+a
2,
BD
2=(3-1)
2+(4a)
2=4+16a
2,
AB
2=3
2+(3a)
2=9+9a
2.
若以A、B、D为顶点的三角形为直角三角形,则分三种情况讨论:
①若∠ADB=90°,则AD
2+BD
2=AB
2,
∴1+a
2+4+16a
2=9+9a
2,
∴a=±

;
②若∠DAB=90°,则AD
2+AB
2=BD
2,
∴1+a
2+9+9a
2=4+16a
2,
∴a=±1;
③若∠ABD=90°,则BD
2+AB
2=AD
2,
∴4+16a
2+9+9a
2=1+a
2,
a无解.
综上,若以A,B,D为顶点的三角形为直角三角形,则a
1=

,a
2=-

,a
3=1,a
4=-1;
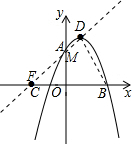
(3)在抛物线上存在点M,能够使∠DBO=∠MDB.
如图,∵OA=OB=3,
∴-3a=3,
∴a=-1.
∴A(0,3),D(1,4),B(3,0).
若点M在x≥1的抛物线上时,∵∠DBO=∠MDB,∴MD∥OB,又点M是抛物线上的点,∴点D与点M重合,不符合题意.
∴点M在x<1的抛物线上.
如图,延长DM交x轴于点F,连接BD.设F(x,0).
∵∠DBO=∠MDB,
∴FD=FB.
∴(1-x)
2+4
2=(3-x)
2,解得x=-2.则F(-2,0).
易求直线FD的方程为:y=

x+

.
则
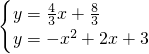
,
解得
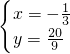
或
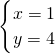
(舍去),
即M(-

,

).
分析:(1)令x=0求得点A的坐标,令y=0来求点B、C的坐标;把抛物线方程转化为顶点式,直接写出点D的坐标;
(2)根据点A、B、D的坐标,利用两点间的距离公式易求AD
2=1+a
2,BD
2=4+16a
2,AB
2=9+9a
2.然后分别以AD、BD、AB为斜边来求相应的a的值;
(3)由OA=OB易求D(1,4),B(3,0).若点M在x≥1的抛物线上时,因为∠DBO=∠MDB,所以MD∥OB,又点M是抛物线上的点,所以点D与点M重合,不符合题意.故点M在x<1的抛物线上.如图,延长DM交x轴于点F,连接BD.设F(x,0).根据两点间的距离公式可以求得点F的坐标,根据点F、D的坐标易求直线FD的方程,由该方程结合抛物线方程列出方程组,即可求得点M的坐标.
点评:本题考查了二次函数综合题.其中涉及到的知识点有二次函数图象上点的坐标特征,勾股定理,待定系数法求一次函数解析式等.在求有关动点问题时要注意分析题意分情况讨论结果.

 如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.
如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D. ;
; ,a2=-
,a2=- ,a3=1,a4=-1;
,a3=1,a4=-1;
 x+
x+ .
.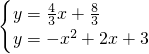 ,
,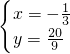 或
或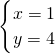 (舍去),
(舍去), ,
, ).
).

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).