
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
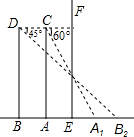 如图所示,细心的王聪站立在镜子EF前的A处时,此时他看自己的脚在镜中的像A1的俯角为60°;如果王聪向后退0.3米到B处,这时他看自己的脚在镜中的像B1的俯角为45°.求王聪的眼睛到地面的距离BD.(结果精确到0.01米,参考数据:$\sqrt{3}≈1.73$)
如图所示,细心的王聪站立在镜子EF前的A处时,此时他看自己的脚在镜中的像A1的俯角为60°;如果王聪向后退0.3米到B处,这时他看自己的脚在镜中的像B1的俯角为45°.求王聪的眼睛到地面的距离BD.(结果精确到0.01米,参考数据:$\sqrt{3}≈1.73$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com