练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．计算：
    2$\frac{5}{9}$-1$\frac{1}{3}$=
    3$\frac{2}{3}$-1$\frac{1}{6}$+$\frac{2}{3}$=
    6$\frac{2}{3}$×3$\frac{1}{4}$=
    3$\frac{1}{3}$÷$\frac{4}{9}$×1$\frac{1}{3}$=

    分析 原式利用加减，乘除法则计算即可得到结果．

    解答 解：原式=1$\frac{2}{9}$；
    原式=3$\frac{1}{6}$；
    原式=$\frac{20}{3}$×$\frac{13}{4}$=$\frac{65}{3}$；
    原式=$\frac{10}{3}$×$\frac{9}{4}$×$\frac{4}{3}$=10．

    点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

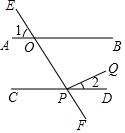    11．如图，直线AB、CD被直线EF所截，交点为O、P，PQ⊥EF，垂足为P，如果∠1=60°，∠2=30°，那么直线AB、CD平行吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，直线1表示铁路，A、B两点表示某工厂两个生产区，若要在铁路旁修建一个货仓C，使货仓C到两个生产区A，B的距离之和最短，则这样的点C的位置（　　）
    A．有1处B．有2处C．有4处D．不存在

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知：如图，在△ABC中，∠C=90°，AE平分∠CAB，且BE2=DE•AE．求证：BE⊥AE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．（1）如图，在数轴上点A表示的数是-1，点B表示的数是2$\frac{2}{3}$；
    （2）请在数轴上用点C表示数-2.5；
    （3）如果该数轴上点D与点C之间的距离是3，那么点D表示的数是0.5或-5.5．

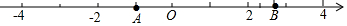
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列说法中，错误的是（　　）
    A．长度为1的向量叫做单位向量
    B．如果k≠0，且$\overrightarrow{a}$≠$\overrightarrow{0}$，那么k$\overrightarrow{a}$的方向与$\overrightarrow{a}$的方向相同
    C．如果k=0或$\overrightarrow{a}$=$\overrightarrow{0}$，那么k$\overrightarrow{a}$=$\overrightarrow{0}$
    D．如果$\overrightarrow{a}$=$\frac{5}{2}$$\overrightarrow{c}$，$\overrightarrow{b}$=$\frac{1}{2}$$\overrightarrow{c}$，其中$\overrightarrow{c}$是非零向量，那么$\overrightarrow{a}$∥$\overrightarrow{b}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算 
    （1）（2a）2     
    （2）x6÷x4     
    （3）x0-（-1）2       
    （4）3x•2xy
    （5）（x+2）（x+3）
    （6）$\frac{m+3}{m+2}$-$\frac{1}{m+2}$   
    （7）（a+1）2-a（a-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

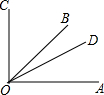    10．如图，已知∠COA=90°，∠COD比∠DOA大n°，且OB是∠COA的平分线．
    （1）若n=36，求∠BOD的度数；
    （2）直接用n的式子表示∠BOD为$\frac{1}{2}$n度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知△ABC的三边满足a2-2bc-c2+2ab=0，判断△ABC的形状并说明理由．

    查看答案和解析>>

    同步练习册答案