
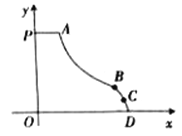
【题目】如图所示的是一种新型的滑梯的示意图,其中线段PA是长为![]() 米的平台,滑道AB是反比例丽数图象的部分,滑道 BCD是二次函数y=-(x-5)2+2图象的部分,两滑道的连接点B为抛物线的顶点,且点C的横坐标为6.
米的平台,滑道AB是反比例丽数图象的部分,滑道 BCD是二次函数y=-(x-5)2+2图象的部分,两滑道的连接点B为抛物线的顶点,且点C的横坐标为6.
(1)求滑道AB所在曲线的解析式;
(2)问小刚同学从点A滑到点C时,其下降的高度为多少米?
【答案】(1)y=![]() ;(2)5米.
;(2)5米.
【解析】
(1)由点B为抛物线顶点可得点B坐标,根据点B为两滑道连接点,可把点B坐标代入反比例函数式y=![]() ,即可得出滑道AB所在曲线解析式;
,即可得出滑道AB所在曲线解析式;
(2)由PA为![]() m,可得点A横坐标,代入反比例函数式可得点A纵坐标,即点A高度,把点C横坐标代入二次函数解析式,可得点C纵坐标,即点C高度,两高度相减,即为小刚下降高度.
m,可得点A横坐标,代入反比例函数式可得点A纵坐标,即点A高度,把点C横坐标代入二次函数解析式,可得点C纵坐标,即点C高度,两高度相减,即为小刚下降高度.
(1)∵点B为抛物线y=-(x-5)2+2顶点,
∴点B坐标(5,2),
∵点B为两滑道连接点,
∴点B在曲线上,
设曲线解析式为y=![]() ,把点B坐标代入反比例函数式,
,把点B坐标代入反比例函数式,
得k=10,即滑道AB所在曲线解析式为y=![]() ;
;
(2)∵PA为![]() m,
m,
∴点A横坐标为![]() ,代入反比例函数式,
,代入反比例函数式,
得点A纵坐标为6,即点A高度;
把点C横坐标6代入y=-(x-5)2+2,得
y=1,即点C高度为1m,
∴从点A到点C的垂直高度为6-1=5m,即小刚同学从点A滑到C点下降的高度为5米.


科目:初中数学 来源: 题型:
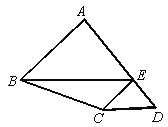
【题目】如图,在四边形ABCD 中,点E在AD上,EC∥AB,EB∥DC,若△ABE面积为5,△ECD的面积为1,则△BCE的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP.
(1)填空:抛物线的解析式为 ,点C的坐标 ;
(2)点P在抛物线上运动,若△AQP∽△AOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
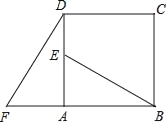
【题目】如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
查看答案和解析>>
科目:初中数学 来源: 题型:
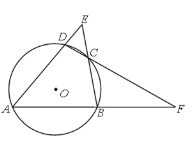
【题目】如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠A=50°,∠E=45°,则∠F=____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
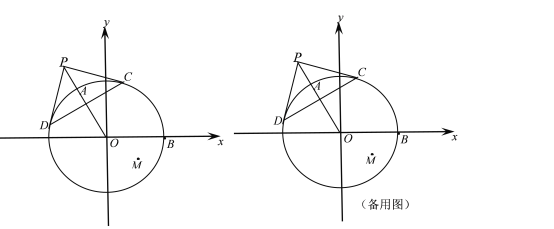
【题目】如图,在平面直角坐标系xoy中,⊙O的圆心O在坐标原点,半径OB在x轴正半轴上,点P是⊙O外一点,连接PO,与⊙O交于点A,PC、PD是⊙O的切线,切点分别为点C、点D,AO=OB=2,∠POB=120°,点M 坐标为(1,-![]() ).
).
(1)求证:OP⊥CD;
(2)连结OM,求∠AOM的大小;
(3) 如果点E在x轴上,且△ABE与△AOM相似,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com