
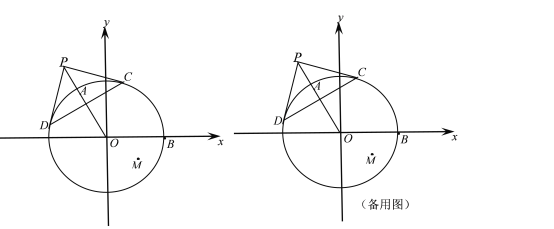
【题目】如图,在平面直角坐标系xoy中,⊙O的圆心O在坐标原点,半径OB在x轴正半轴上,点P是⊙O外一点,连接PO,与⊙O交于点A,PC、PD是⊙O的切线,切点分别为点C、点D,AO=OB=2,∠POB=120°,点M 坐标为(1,-![]() ).
).
(1)求证:OP⊥CD;
(2)连结OM,求∠AOM的大小;
(3) 如果点E在x轴上,且△ABE与△AOM相似,求点E的坐标.
【答案】(1)见解析;(2)150°;(3) E(4,0)或(8,0).
【解析】
(1)根据直线与圆相切的性质证明Rt△PDO ≌Rt△PCO,就可以证明OP⊥CD(2)连接OM,利用三角函数值解直角三角形即可(3)根据△ABE与△AOM相似,可以得到边,角的关系,进而得到点的坐标.
(1)连接OD、OC
∵PC、PD是⊙O的切线
∴∠PDO=∠PCO=90° ,PC=PD
∵在Rt△PDO 与Rt△PCO中
![]() ∴Rt△PDO ≌Rt△PCO(HL)
∴Rt△PDO ≌Rt△PCO(HL)
∴∠CPO=∠DPO
∵PC=PD,∠CPO=∠DPO
∴OP⊥CD
(2)连接OM,作MH⊥x轴
∵在Rt△HMO中 ∴tan∠HOM=![]() =
=![]() ∴ ∠HOM=30°
∴ ∠HOM=30°
∴ ∠AOM=∠HOM+∠POB=30°+120°=150°
(3)由OA=OB=2,∠AOB=120°,得∠ABO=30°
若点E在点B左侧时,不论∠AEB和∠EAB哪个
角等于150°,此时三角形内角和都大于180°
则点E只能在点B右侧
∵∠ABO=30°∴∠ABE=∠AOM=150°
若△ABE与△AOM相似存在两种情况
①△AOM ∽△ABE ∴![]() =
=![]()
∴ BE=2
∴E(4,0)
②△AOM ∽△EBA ∴![]() =
=![]()
∴ BE=6
∴E(8,0)
综上所述:E(4,0)或(8,0).


科目:初中数学 来源: 题型:
【题目】如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=4,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
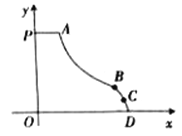
【题目】如图所示的是一种新型的滑梯的示意图,其中线段PA是长为![]() 米的平台,滑道AB是反比例丽数图象的部分,滑道 BCD是二次函数y=-(x-5)2+2图象的部分,两滑道的连接点B为抛物线的顶点,且点C的横坐标为6.
米的平台,滑道AB是反比例丽数图象的部分,滑道 BCD是二次函数y=-(x-5)2+2图象的部分,两滑道的连接点B为抛物线的顶点,且点C的横坐标为6.
(1)求滑道AB所在曲线的解析式;
(2)问小刚同学从点A滑到点C时,其下降的高度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
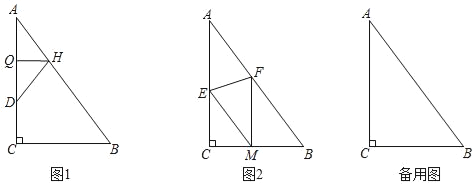
【题目】在△ABC中,∠ACB=90°,AB=25,BC=15.
(1)如图1,折叠△ABC使点A落在AC边上的点D处,折痕交AC、AB分别于Q、H,若S△ABC=9S△DHQ,则HQ= .
(2)如图2,折叠△ABC使点A落在BC边上的点M处,折痕交AC、AB分别于E、F.若FM∥AC,求证:四边形AEMF是菱形;
(3)在(1)(2)的条件下,线段CQ上是否存在点P,使得△CMP和△HQP相似?若存在,求出PQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠ADC是否是直角,并说明理由;
(2)试求四边形草坪ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com