
����Ŀ��2018��10��23�գ�����Ĵ�����ʽ��ͨ����Ϊ��ب���������ϵ�һ�������ķ羰.�������幤�������Ķ��������˸�������һ�������˹��������ν������ͺ������������˹����ϵ�A��Ͷ��˹����ϵ�B���ľ���ԼΪ5.6ǧ�ף���C�������˹��������Ĵ����ϵ�һ�㣬A��B��C��һ��ֱ���ϣ���ͼ��һ�ҹ۹�������![]() �δ�ֱ�ķ����У�����P��ʱ�۲������˹������ֱ���
�δ�ֱ�ķ����У�����P��ʱ�۲������˹������ֱ���![]() ��۹����
��۹����![]() �ļнǡ�DPA=18�㣬��DPB=53�㣬���ʱ�۹������AC�εľ���
�ļнǡ�DPA=18�㣬��DPB=53�㣬���ʱ�۹������AC�εľ���![]() �ij���
�ij���
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

���𰸡�5.6ǧ��
��������
��PD�ij�Ϊxǧ�ף�DA�ij�Ϊyǧ�ף���Rt��PAD���������еĶ���õ�tan18��=![]() ����y=0.33x��ͬ����Rt��PDB�еõ�y+5.6=1.33x������0.33x+5.6=1.33x��Ȼ��ⷽ�����x���ɣ�
����y=0.33x��ͬ����Rt��PDB�еõ�y+5.6=1.33x������0.33x+5.6=1.33x��Ȼ��ⷽ�����x���ɣ�
��PD�ij�Ϊxǧ�ף�DA�ij�Ϊyǧ�ף�
��Rt��PAD��tan��DPA=![]() ��
��
��tan18��=![]() ��
��
��y=0.33x��
��Rt��PDB��tan��DPB=![]() ��
��
��tan53��=![]() ��
��
��y+5.6=1.33x��
��0.33x+5.6=1.33x�����x=5.6��
�𣺴�ʱ�۹������AC�εľ���PD�ij�Ϊ5.6ǧ�ף�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ˮƽ�IJ�����ߣ����м�ͥ�γ���ӵ������������.��ͳ�ƣ�ijС��2015���ӵ�м�ͥ�γ�64����2017���ͥ�γ���ӵ�����ﵽ100��.
��1������С��2015���2018���ͥ�γ�ӵ��������ƽ�������ʶ���ͬ�����С����2018���ͥ�γ����ﵽ��������
��2��Ϊ�˻���ͣ��ì�ܣ���С������Ͷ��15��Ԫ�ٽ������ɸ�ͣ��λ.�ݲ��㣬������÷ֱ�Ϊ���ڳ�λ5000Ԫ/����¶�쳵λ1000Ԫ/�������ǵ�ʵ�����أ��ƻ�¶�쳵λ���������������ڳ�λ��2���������������ڳ�λ��2.5�������С�����ɽ����ֳ�λ�����ٸ�����д�����п��ܵķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
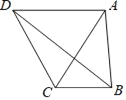
����Ŀ����ͼ�����ı���ABCD�У�AB��6��BC��4����AC��AD���ҡ�ACD��60�㣬��Խ���BD�ij������ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
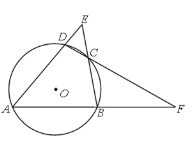
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��AD��BC���ӳ����ཻ�ڵ�E��AB��DC���ӳ����ཻ�ڵ�F������A��50�㣬��E��45�㣬���F=____�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
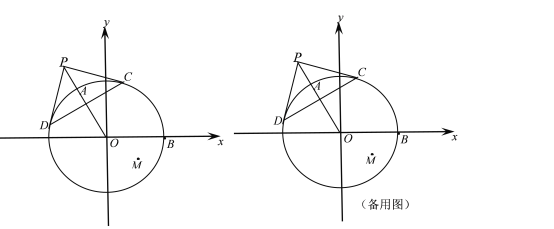
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У���O��Բ��O������ԭ�㣬�뾶OB��x���������ϣ���P�ǡ�O��һ�㣬����PO�����O���ڵ�A��PC��PD�ǡ�O�����ߣ��е�ֱ�Ϊ��C����D��AO��OB=2����POB��120�㣬��M ����Ϊ(1����![]() ����
����
(1)��֤��OP��CD��
(2)����OM�����AOM�Ĵ�С��
(3) �����E��x���ϣ��ҡ�ABE���AOM���ƣ����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AB=AC����BAC=����ֱ��l������A����������B���C������C����ֱ��l�ĶԳƵ�Ϊ��D������BD��CD��
��1����ͼ1��
����֤����![]() ���Ե�
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ��.
Ϊ�뾶��Բ��.
��ֱ��д����BDC�Ķ������ú�����ʽ�ӱ�ʾ��Ϊ___________.
��2����ͼ2������=60��ʱ������D��BD�Ĵ�����ֱ��l���ڵ�E����֤��AE=BD��
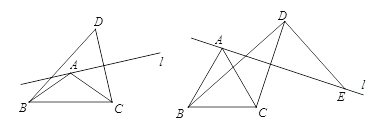
ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽�������з��̣�����Ӧ�ڷ�����������ͬʱ����4���ǣ�������
A. x2��2x��5 B. x2+4x��5 C. 2x2��4x��5 D. 4x2+4x��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰ����߳��ı�Ϊ3:4:5�������γ�Ϊ��ȫ�����Σ�������A������ȫ��������ֱ����������.������B������A�������⣬��д������B��______________________����д��һ������(���������ж�����B�Ǵ����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ծ���ABCD�ĶԽ���ACΪһ�������·���������ACEF���ӳ�AB��EF�ڵ�G����AB��3��BC��4����EG�ij�Ϊ_____��
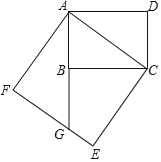
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com