
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
(1)如图1,
①求证:点![]() 在以点
在以点![]() 为圆心,
为圆心,![]() 为半径的圆上.
为半径的圆上.
②直接写出∠BDC的度数(用含α的式子表示)为___________.
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD;
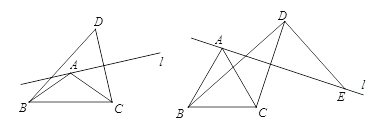
图1 图2
【答案】(1)①证明见解析;②![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)①连结AD,由线段的垂直平分线的性质得AD=AC,AB=AC,故可得AB=AC=AD,从而查得出结论;
②由圆周角定理可得出结论;
(2)连结CE,易证△CDE和△ABC为等边三角形,从而可证![]() ,进而得出结论.
,进而得出结论.
(1)①证明:连接![]() ,如图1.
,如图1.

∵点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上.
为半径的圆上.
②点B,C,D在以A为圆心,AB为半径的圆上,根据弧BC所对的圆周角是圆心角的一半,所以∠BDC=![]() .
.
(2)证明:连接![]() ,如图2.
,如图2.

∵![]() °,
°,
∴![]() °.
°.
∵![]() ,
,
∴![]() °
°![]() °.
°.
∵点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.
∴![]() ,
,![]() °.
°.
∵![]() ,
,![]() °,
°,
∴![]() 是等边三角形.
是等边三角形.
∴![]() ,
,![]() °.
°.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】 某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有______人.
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,平均每人捐款多少元?
(3)在(2)的条件下,把每个学生的捐款数(以元为单位)一一记录下来,则在这组数据中,众数和中位数分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,BN和CM有什么数量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
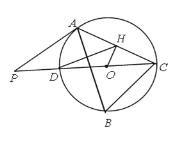
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若OH⊥AC,OH=1,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.
(1)求小球飞行3s时的高度;
(2)问:小球的飞行高度能否达到22m?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
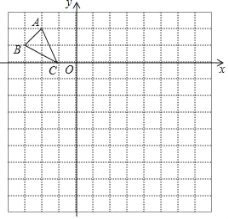
【题目】如图,在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系,格点△ABC(顶点是网格线的交点)的坐标分别是A(﹣2,2),B(﹣3,1),C(﹣1,0).
(1)将△ABC绕点O逆时针旋转90°得到△DEF,画出△DEF;
(2)以O为位似中心,将△ABC放大为原来的2倍,在网格内画出放大后的△A1B1C1,若P(x,y)为△ABC中的任意一点,这次变换后的对应点P1的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李的活鱼批发店以44元/公斤的价格从港口买进一批2000公斤的某品种活鱼,在运输过程中,有部分鱼未能存活,小李对运到的鱼进行随机抽查,结果如表一.由于市场调节,该品种活鱼的售价与日销售量之间有一定的变化规律,表二是近一段时间该批发店的销售记录.
(1)请估计运到的2000公斤鱼中活鱼的总重量;(直接写出答案)
(2)按此市场调节的观律,
①若该品种活鱼的售价定为52.5元/公斤,请估计日销售量,并说明理由;
②考虑到该批发店的储存条件,小李打算8天内卖完这批鱼(只卖活鱼),且售价保持不变,求该批发店每日卖鱼可能达到的最大利润,并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com