Question

【题目】如图，△ABC是等腰三角形，点D是底边BC上异于BC中点的一个点，∠ADE=∠DAC，DE=AC．运用这个图（不添加辅助线）可以说明下列哪一个命题是假命题？（ ）
A.一组对边平行，另一组对边相等的四边形是平行四边形
B.有一组对边平行的四边形是梯形
C.一组对边相等，一组对角相等的四边形是平行四边形
D.对角线相等的平行四边形是矩形

Answer 1

【答案】C
【解析】解：∵△ABC是等腰三角形， ∴AB=AC，∠B=∠C，
在△ADE与△DAC中，
∵ ，
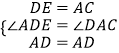∴△ADE≌△DAC，
∴∠E=∠C，
∴∠B=∠E，AB=DE，
但是四边形ABDE不是平行四边形，
故一组对边相等，一组对角相等的四边形是平行四边形说法错误；
故选：C．
【考点精析】认真审题，首先需要了解等腰三角形的性质(等腰三角形的两个底角相等（简称：等边对等角）)，还要掌握平行四边形的判定(两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形)的相关知识才是答题的关键．