
【题目】感知:如图1,在△ABC中,∠ABC=42°,∠ACB=72°,点D是AB上一点,E是AC上一点,BE、CD相交于点F.
(1)若∠ACD=35°,∠ABE=20°,求∠BFC的度数;
(2)若CD平分∠ACB,BE平分∠ABC,求∠BFC的度数;
探究:如图2,在△ABC中,BE平分∠ABC,CD平分∠ACB,写出∠BFC与∠A之间的数量关系,并说明理由;
应用:如图3,在△ABC中,BD平分∠ABC ,CD平分外角∠ACE,请直接写出∠BDC与∠A之间的数量关系.



【答案】(1)121°;(2)∠BFC=90°+![]() ∠A,证明见解析;(3)∠BDC=
∠A,证明见解析;(3)∠BDC=![]() ∠A.
∠A.
【解析】分析:(1)、根据△ABC的内角和定理得出∠A的度数,然后根据∠BEC=∠A+∠ABE得出答案;(2)、根据角平分线的性质得出∠ABE=![]() ∠ABC,∠ACD=
∠ABC,∠ACD=![]() ∠ACB,最后根据三角形外角的性质以及三角形内角和定理得出答案;(3)、根据三角形外角的性质以及三角形内角和定理得出答案.
∠ACB,最后根据三角形外角的性质以及三角形内角和定理得出答案;(3)、根据三角形外角的性质以及三角形内角和定理得出答案.
详解:(1)、∵在△ABC中,∠ABC+∠ACB+∠A=180°,又∵∠ABC=42°,∠ACB=72°,
∴∠A=66°, ∵∠BEC=∠A+∠ABE=20°+66°=86°,
又∵∠BFC=∠ACD+∠BEC=35°+86°=121°;
(2)、结论:∠BFC=90°+![]() ∠A,
∠A,
证明:∵BE平分∠ABC,CD平分∠ACB, ∴∠ABE=![]() ∠ABC,∠ACD=
∠ABC,∠ACD=![]() ∠ACB,
∠ACB,
∵∠BEC=∠A+∠ABE,∠BFC=∠ACD+∠BEC, ∴∠BFC=∠A+∠ACD+∠ABE,
∴∠BFC=∠A+![]() ∠ABC+
∠ABC+![]() ∠ACB, ∵∠A+∠ABC+∠ACB=180°,
∠ACB, ∵∠A+∠ABC+∠ACB=180°,
∴∠BFC=90°+![]() ∠A;
∠A;
(3)∠BDC=![]() ∠A.
∠A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
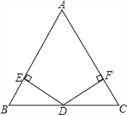
【题目】如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=![]() ,BE=5.
,BE=5.
①求证: ![]() ②求△ABC的周长.
②求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
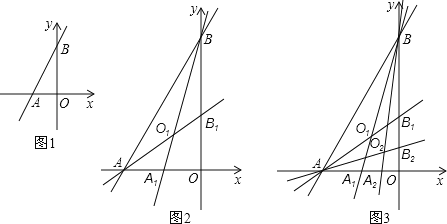
【题目】如图1,一次函数y=2x+4与x轴,y轴分别相交于A,B两点,一次函数图象与坐标轴围成的△ABO,我们称它为此一次函数的坐标三角形.把坐标三角形面积分成相等的二部分的直线叫做坐标三角形的等积线.
(1)求此一次函数的坐标三角形周长以及过点A的等积线的函数表达式;
(2)如图2,我们把第一个坐标三角形△ABO记为第一代坐标三角形.第一代坐标三角形的等积线BA1,AB1记为第一对等积线,它们交于点O1,四边形A1OB1O1称为第一个坐标四边形.求点O1的坐标和坐标四边形A1OB1O1面积;
(3)如图3.第一对等积线与坐标轴构成了第二代坐标三角形△BA1O.△AOB1分别过点A,B作一条平分△BA1O,△AOB1面积的第二对等积线BA2,AB2,相交于点O2,如此进行下去.…,请直接写出On的坐标和第n个坐标四边形面积(用n表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( ) 
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一组对边平行的四边形是梯形
C.一组对边相等,一组对角相等的四边形是平行四边形
D.对角线相等的平行四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,OE⊥AB,OF⊥AC且OE=OF.
(1)如图,当点O在BC边中点时,试说明AB=AC;

(2)如图,当点O在△ABC内部时,且OB=OC,试说明AB与AC的关系;

(3)当点O在△ABC外部时,且OB=OC,试判断AB与AC的关系.(画出图形,写出结果即可,无须说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com