
【题目】在△ABC中,OE⊥AB,OF⊥AC且OE=OF.
(1)如图,当点O在BC边中点时,试说明AB=AC;

(2)如图,当点O在△ABC内部时,且OB=OC,试说明AB与AC的关系;

(3)当点O在△ABC外部时,且OB=OC,试判断AB与AC的关系.(画出图形,写出结果即可,无须说明理由)
【答案】见解析
【解析】试题分析:(1)证△BOE≌△COF,可得∠B=∠C,通过等角对等边,得出AB=AC;
(2)与(1)类似,在证得△BOE≌△COF后,得∠OBE=∠OCF,OB=OC;则∠OBC=∠OCB,可证得∠ABC=∠ACB,根据等角对等边得出AB=AC;
(3)由前两问的解答过程可知,BC的垂直平分线与∠A的角平分线重合时,AB=AC的结论才成立(等腰三角形三线合一).
试题解析:(1)证明:∵OE=OF,OB=OC,∴Rt△OBE≌Rt△OCF(HL),∴∠B=∠C,∴AB=AC.
(2)AB=AC.证明如下:
同(1)可证得Rt△OBE≌Rt△OCF,∴∠OBE=∠OCF.
∵OB=OC,∴∠OBC=∠OCB,∴∠ABC=∠ACB,∴AB=AC.
解:当BC的垂直平分线与∠A的平分线重合时,AB=AC成立,如图①;
当BC的垂直平分线与∠A的平分线不在一条直线上时,结论不成立,如图②.(图形不唯一,符合题意,画图规范即可).



科目:初中数学 来源: 题型:
【题目】感知:如图1,在△ABC中,∠ABC=42°,∠ACB=72°,点D是AB上一点,E是AC上一点,BE、CD相交于点F.
(1)若∠ACD=35°,∠ABE=20°,求∠BFC的度数;
(2)若CD平分∠ACB,BE平分∠ABC,求∠BFC的度数;
探究:如图2,在△ABC中,BE平分∠ABC,CD平分∠ACB,写出∠BFC与∠A之间的数量关系,并说明理由;
应用:如图3,在△ABC中,BD平分∠ABC ,CD平分外角∠ACE,请直接写出∠BDC与∠A之间的数量关系.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,王虎使一长为4 cm,宽为3 cm的长方形木板,在桌面上做无滑动地翻滚(顺时针方向),木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是()
A.相等的角是对顶角
B.在平面内,经过一点有且只有一条直线与已知直线平行
C.两条直线被第三条直线所截,内错角相等
D.在平面内,经过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.﹣1的平方根是﹣1
B.4的平方根是2
C.如果一个数有平方根,那么这个数的平方根一定有两个
D.任何一个非负数的立方根都是非负数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
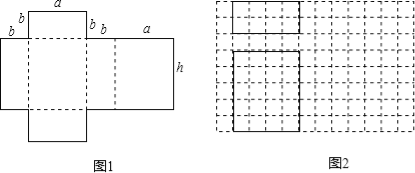
(1)这个几何体模型的名称是 .
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足![]() a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com