
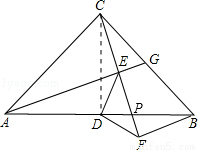
已知等腰Rt△ABC中,∠ACB=90°,AC=BC,点G在BC上,连接AG,过C作CF⊥AG,垂足为点E,过点B作BF⊥CF于点F,点D是AB的中点,连接DE、DF
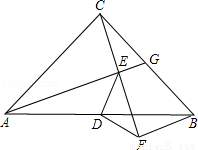
(1)若∠CAG=30°,EG=1,求BG的长;
(2)求证:∠AED=∠DFE.
(1)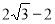 ;(2)证明见试题解析.
;(2)证明见试题解析.
【解析】
试题分析:(1)首先根据勾股定理求出CE的长,进而得到AC的长,因为AC=BC,所以BC可求,利用BH=BC﹣CG计算即可;
(2)连接CD,通过证明分别证明△ACE≌△CBF和△DCE≌△DBF,利用全等三角形的性质即可证明∠AED=∠DFE.
解答:(1)【解析】
∵∠ACE=∠ECG=30°,EG=1,sin30°=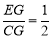 ,∴CG=2,∴CE=
,∴CG=2,∴CE=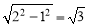 ,
,
∵sin30°=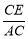 ,∴AC=
,∴AC= ,∴BC=
,∴BC= ,∴BG=
,∴BG=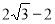 ;
;
(2)证明:连接CD,
在△ACE和△CBF中,∵∠AEC=∠CFB,∠CAE=∠FCB,AC=BC,∴△ACE≌△CBF(AAS),∴CE=BF,
∵等腰RT△ABC中,点D是AB的中点,∴CD=BD,
∵CD⊥BD,∠DCE+∠DPC=∠FBP+∠FPB=90°,∴∠DCE=∠DBF,
在△DCE和△DBF中,
∵CF=BF,∠DCE=∠DBF,DC=BD,∴△DCE≌△DBF(SAS),∴∠CED=∠BFD,
∵∠AEC=∠CFB=90°,∴∠AED=∠DFE.
考点:1.全等三角形的判定与性质;2.等腰直角三角形;3.解直角三角形.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:2014-2015学年重庆市九年级上学期期中考试数学试卷(解析版) 题型:选择题
在 ,
, ,
,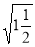 ,
, 中最简二次根式的个数是 ( )
中最简二次根式的个数是 ( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市等九年级模拟联考数学试卷(解析版) 题型:填空题
如图,直线 与x轴、y轴分别交于点A、B,已知点P是第一象限内的点,由点P、O、B组成了一个含60°的直角三角形,则点P的坐标为 .
与x轴、y轴分别交于点A、B,已知点P是第一象限内的点,由点P、O、B组成了一个含60°的直角三角形,则点P的坐标为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市沙坪坝区九年级上学期期中联考数学试卷(解析版) 题型:选择题
如图,已知在△ABC,P为AB上一点,连结CP,不能判断△ABC~△ACP的是( )

A.∠ACP=∠B B.∠APC=∠ACB
C. =
= D.
D. =
=
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市沙坪坝区九年级上学期期中联考数学试卷(解析版) 题型:选择题
如图,双曲线 经过直角三角形
经过直角三角形 斜边
斜边 的中点
的中点 ,与直角边
,与直角边 相交于点
相交于点 .过
.过 作
作 ⊥
⊥ 交
交 于点
于点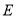 ,若△
,若△ 的面积为
的面积为 ,则
,则 的值是 ( ).
的值是 ( ).

A.1 B.2 C.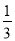 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市校七年级12月月考数学试卷(解析版) 题型:选择题
去括号正确的是( )
A.-(a+b-c)=-a+b-c
B.-2(a+b-3c)=-2a-2b+6c
C.-(-a-b-c)=-a+b+c
D.-(a-b-c)=-a+b-c
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市校八年级12月月考数学试卷(解析版) 题型:选择题
古希腊著名的毕达哥拉斯学派把1,3,6,10 …这样的数称为“三角形数”,而把1,4,9,16 …这样的数称为“正方数”. 从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A.20=6+14 B.25=9+16 C.36=16+20 D.49=21+28
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com