(1)如图1.已知∠AOB和C.D两点.在∠ADB的内部求作一点P.使得PC=PD且到∠AOB两边的距离相等(保留作图痕迹.不写作法)(2)如图2.在直线m上确定一点P.使得PA+PB最小．题目和参考答案——青夏教育精英家教网—

20．（1）如图1，已知∠AOB和C、D两点，在∠ADB的内部求作一点P，使得PC=PD且到∠AOB两边的距离相等（保留作图痕迹，不写作法）
（2）如图2，在直线m上确定一点P，使得PA+PB最小．

分析（1）先作CD的垂直平分线和∠AOB的平分线，它们的交点为P点，则根据线段垂直平分线的性质和角平分线的性质得到PC=PD，且P到∠AOB两边的距离相等．
（2）过A作直线m的垂线，在垂线上取点A′，使直线m是AA′的垂直平分线，连接BA′即可得出P点位置．

解答解：（1）点P即为所求；
．

（2）点P即为所求．

点评此题主要考查了复杂作图，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．轴对称最短路线问题，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．

练习册系列答案

名师点拨课时作业甘肃教育出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

10．

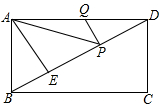如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为3$\sqrt{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．（1）计算：$\sqrt{16}$+（2-$\sqrt{2}$）⁰-（-$\frac{1}{2}$）^-2+|-1|
（2）计算：2$\sqrt{12}$•（3$\sqrt{48}$-4$\sqrt{\frac{1}{8}}$-3$\sqrt{27}$）

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．已知分式$\frac{x-3}{{x}^{2}-5x+a}$，当x=2时，分式无意义，则a=6；若对于任意x的值，分式均有意义，则a的取值范围是a＞$\frac{25}{4}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

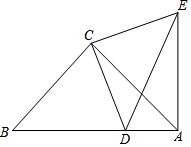如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB上一点．
（1）求证：△ACE≌△BCD
（2）求证：AD²+BD²=DE²．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

5．一组数据2，6，-4，5，-2，|-4|，2，则这组数据的众数是（　　）

A．

B．

C．

D．

-4

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．

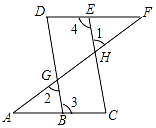如图，点E在直线DF上，点B在直线AC上，若∠1=∠2，∠3=∠4，求证：∠A=∠F
解：∵∠1=∠2（已知）
∠2=∠DGF （对顶角相等）
∴∠1=∠DGF  （等量代换  ）
∴BD∥CE （同位角相等，两直线平行）
∴∠3+∠C=180°  （两直线平行，同旁内角互补）
又∵∠3=∠4（已知）
∴∠4+∠C=180°
∴AC∥DF（同旁内角互补，两直线平行）
∴∠A=∠F   （两直线平行，内错角相等）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．如果一个点能与另外两个点能构成直角三角形，则称这个点为另外两个点的勾股点，例如：矩形ABCD中，点C与A，B两点可构成直角三角形ABC，则称点C为A，B两点的勾股点，同样，点D也是A，B两点的勾股点．如图，矩形ABCD中，请在边CD上作出A，B两点的勾股点（点C和点D除外）（要求：尺规作图，保留作图痕迹，不要求写作法）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

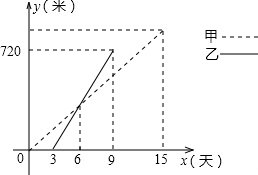如皋某乡镇决定对A、B两村之间的公路进行改造，并有甲工程队从A村向B村方向修筑，乙工程队从B村向A村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务由甲工程队单独完成，直到公路修通．下图是甲乙两个工程队修公路的长度y（米）与施工时间x（天）之间的函数图象，请根据图象所提供的信息解答下列问题：
（1）乙工程队每天修公路120米．
（2）分别求甲、乙工程队修公路的长度y（米）与施工时间x（天）之间的函数关系式．
（3）若该项工程由甲、乙两工程队一直合作施工，需几天完成？

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学