
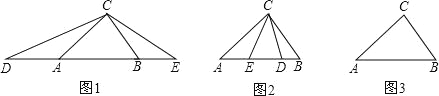
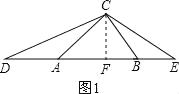
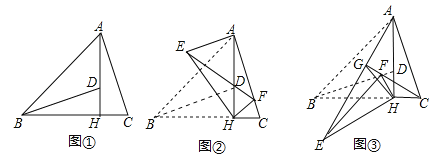
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌдкЁїABCжаЃЌABЃОACЃОBCЃЌЁЯACB=80ЁуЃЌЕуDЁЂEЗжБ№дкЯпЖЮBAЁЂABЕФбгГЄЯпЩЯЃЌЧвAD=ACЃЌBE=BCЃЌдђЁЯDCE= ЃЛ
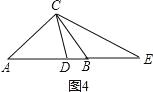
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌдкЁїABCжаЃЌABЃОACЃОBCЃЌЁЯACB=80ЁуЃЌЕуDЁЂEЗжБ№дкБпABЩЯЃЌЧвAD=ACЃЌBE=BCЃЌЧѓЁЯDCEЕФЖШЪ§ЃЛ
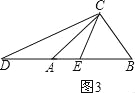
ЃЈ3ЃЉдкЁїABCжаЃЌABЃОACЃОBCЃЌЁЯACB=80ЁуЃЌЕуDЁЂEЗжБ№дкжБЯпABЩЯЃЌЧвAD=ACЃЌBE=BCЃЌдђЁЯЧѓDCEЕФЖШЪ§ЃЈжБНгаДГіД№АИЃЉЃЛ
ЃЈ4ЃЉШчЭМЃЈ3ЃЉЃЌдкЁїABCжаЃЌAB=14ЃЌAC=15ЃЌBC=13ЃЌЕуDЁЂEдкжБЯпABЩЯЃЌЧвAD=ACЃЌBE=BCЃЎЧыИљОнЬтвтАбЭМаЮВЙЛЭъећЃЌВЂдкЭМаЮЕФЯТЗНжБНгаДГіЁїDCEЕФУцЛ§ЃЎЃЈШчЙћгаЖржжЧщПіЃЌЭМаЮВЛЙЛгУЧыздМКЛГіЃЌИїжжЧщПігУвЛИіЭМаЮЕЅЖРБэЪОЃЉЃЎ
ЁОД№АИЁП(1)ЁЂ130ЁуЃЛ(2)ЁЂ50ЁуЃЛ(3)ЁЂ40ЁуЃЛ(4)ЁЂ252Лђ84Лђ96Лђ72.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃК(1)ЁЂИљОнЕШбќШ§НЧаЮЕФаджЪЕУЕНЁЯACD=ЁЯDЃЌЁЯBCE=ЁЯEЃЌгЩШ§НЧаЮЕФФкНЧКЭЕУЕНЁЯCAB+ЁЯCBA=100ЁуЃЌИљОнШ§НЧаЮЕФЭтНЧЕФаджЪЕУЕНЁЯCDA+ЁЯBCE=![]() ЃЈЁЯCAB+ЁЯCBAЃЉ=50ЁуЃЌМДПЩЕУЕННсТлЃЛ
ЃЈЁЯCAB+ЁЯCBAЃЉ=50ЁуЃЌМДПЩЕУЕННсТлЃЛ
(2)ЁЂИљОнШ§НЧаЮЕФФкНЧКЭКЭЭтНЧЕФаджЪМДПЩЕУЕННсТлЃЛ(3)ЁЂЕуDЁЂEЗжБ№дкжБЯпABЩЯЃЌГ§ШЅЃЈ1ЃЉЃЈ2ЃЉСНжжЧщПіЃЌЛЙгаСНжжЧщПіЃЌШчЭМ3ЃЌгЩ(1)жЊЃЌЁЯD=![]() CABЃЌгЩЃЈ2ЃЉжЊЁЯCEB=
CABЃЌгЩЃЈ2ЃЉжЊЁЯCEB=![]() ЃЌСаЗНГЬМДПЩЧѓЕУНсЙћЃЎЃЈ4ЃЉдкЁїABCжаЃЌAB=14ЃЌAC=15ЃЌBC=13ЃЌЙ§CзїCFЁЭABгыFЃЌИљОнЙДЙЩЖЈРэЧѓЕУABБпЩЯЕФИпCF=12ЃЌШЛКѓИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЧПДѓЕФНсТлЃЎ
ЃЌСаЗНГЬМДПЩЧѓЕУНсЙћЃЎЃЈ4ЃЉдкЁїABCжаЃЌAB=14ЃЌAC=15ЃЌBC=13ЃЌЙ§CзїCFЁЭABгыFЃЌИљОнЙДЙЩЖЈРэЧѓЕУABБпЩЯЕФИпCF=12ЃЌШЛКѓИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЧПДѓЕФНсТлЃЎ
ЪдЬтНтЮіЃК(1)ЁЂЁпAD=ACЃЌBE=BCЃЌ ЁрЁЯACD=ЁЯDЃЌЁЯBCE=ЁЯEЃЌ ЁпЁЯACB=80ЁуЃЌ
ЁрЁЯCAB+ЁЯCBA=100ЁуЃЌ ЁрЁЯCDA+ЁЯBCE=![]() ЃЈЁЯCAB+ЁЯCBAЃЉ=50ЁуЃЌ ЁрЁЯDCE=130ЁуЃЌ
ЃЈЁЯCAB+ЁЯCBAЃЉ=50ЁуЃЌ ЁрЁЯDCE=130ЁуЃЌ
(2)ЁЂЁпЁЯACB=80ЁуЃЌ ЁрЁЯA+ЁЯB=100ЁуЃЌ ЁпAD=ACЃЌBE=BCЃЌ ЁрЁЯACD=ЁЯADCЃЌЁЯBEC=ЁЯBCEЃЌ
ЁрЁЯADC=![]() ЃЌЁЯBEC=
ЃЌЁЯBEC=![]() ЃЌ ЁрЁЯADC+ЁЯBEC=180ЁуЉ
ЃЌ ЁрЁЯADC+ЁЯBEC=180ЁуЉ![]() ЃЈЁЯA+ЁЯBЃЉ=130ЁуЃЌЁрЁЯDCE=50ЁуЃЛ
ЃЈЁЯA+ЁЯBЃЉ=130ЁуЃЌЁрЁЯDCE=50ЁуЃЛ
(3)ЁЂЕуDЁЂEЗжБ№дкжБЯпABЩЯЃЌГ§ШЅЃЈ1ЃЉЃЈ2ЃЉСНжжЧщПіЃЌЛЙгаСНжжЧщПіЃЌШчЭМ3ЃЌ
гЩЃЈ1ЃЉжЊЃЌЁЯD=![]() CABЃЌгЩЃЈ2ЃЉжЊЁЯCEB=
CABЃЌгЩЃЈ2ЃЉжЊЁЯCEB=![]() ЃЌ ЁрЁЯCEB=ЁЯD+ЁЯDCEЃЌ
ЃЌ ЁрЁЯCEB=ЁЯD+ЁЯDCEЃЌ
Ёр![]() =
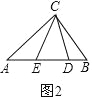
=![]() CAB+ЁЯDCEЃЌ ЁрЁЯDCE=40ЁуЃЌ ШчЭМ4ЃЌЭЌРэЁЯDCE=40ЁуЃЛ
CAB+ЁЯDCEЃЌ ЁрЁЯDCE=40ЁуЃЌ ШчЭМ4ЃЌЭЌРэЁЯDCE=40ЁуЃЛ
(4)ЁЂдкЁїABCжаЃЌAB=14ЃЌAC=15ЃЌBC=13ЃЌ Й§CзїCFЁЭABгыFЃЌ
(5)дђAC2ЉAF2=BC2ЉBF2ЃЌМД152ЉAF2=132ЉЃЈ14ЉAFЃЉ2ЃЌ НтЕУЃКAF=9ЃЌ ЁрCF=12ЃЌ
ЂйШчЭМ1ЃЌDE=AB+AC+BC=42ЃЌ ЁрSЁїCDE=![]() ЁС42ЁС12=252ЃЛ
ЁС42ЁС12=252ЃЛ
ЂкШчЭМ2ЃЌDE=AC+BCЉAB=14ЃЌ ЁрSЁїCDE=![]() ЁС14ЁС12=84ЃЛ
ЁС14ЁС12=84ЃЛ
ЂлШчЭМ3ЃЌDE=AC+ABЉBC=16ЃЌ ЁрSЁїCDE=![]() ЁС16ЁС12=96ЃЛ
ЁС16ЁС12=96ЃЛ
ЂмШчЭМ4ЃЌDE=AB+BCЉAC=12ЃЌ ЁрSЁїCDE=![]() ЁС12ЁС12=72ЃЎ
ЁС12ЁС12=72ЃЎ


 Ш§ЕувЛВтПьРжжмМЦЛЎЯЕСаД№АИ
Ш§ЕувЛВтПьРжжмМЦЛЎЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
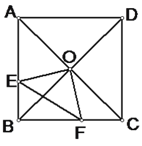
ЁОЬтФПЁПдке§ЗНаЮABCDжаЃЌOЪЧЖдНЧЯпЕФНЛЕуЃЌЙ§OзїOEЁЭOFЃЌЗжБ№НЛABЁЂBCгкEЁЂFЃЌШєAEЃН4ЃЌCFЃН3ЃЌ
ЃЈ1ЃЉЧѓжЄЃКOE=OF
ЃЈ2ЃЉЧѓ EFЕФГЄ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
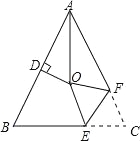
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌAB=ACЃЌЁЯBAC=54ЁуЃЌЕуDЮЊABжаЕуЃЌЧвODЁЭABЃЌЁЯBACЕФЦНЗжЯпгыABЕФДЙжБЦНЗжЯпНЛгкЕуOЃЌНЋЁЯCбиEFЃЈEдкBCЩЯЃЌFдкACЩЯЃЉелЕўЃЌЕуCгыЕуOЧЁКУжиКЯЃЌдђЁЯOECЮЊ ЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
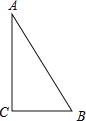
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10cmЃЌBC=6cmЃЌШєЖЏЕуPДгЕуCПЊЪМЃЌАДCЁњAЁњBЁњCЕФТЗОЖдЫЖЏЃЌЧвЫйЖШЮЊУПУы1cmЃЌЩшГіЗЂЕФЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉГіЗЂ2УыКѓЃЌЧѓЁїABPЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕБtЮЊМИУыЪБЃЌBPЦНЗжЁЯABCЃЛ
ЃЈ3ЃЉЮЪtЮЊКЮжЕЪБЃЌЁїBCPЮЊЕШбќШ§НЧаЮЃП
ЃЈ4ЃЉСэгавЛЕуQЃЌДгЕуCПЊЪМЃЌАДCЁњBЁњAЁњCЕФТЗОЖдЫЖЏЃЌЧвЫйЖШЮЊУПУы2cmЃЌШєPЁЂQСНЕуЭЌЪБГіЗЂЃЌЕБPЁЂQжагавЛЕуЕНДяжеЕуЪБЃЌСэвЛЕувВЭЃжЙдЫЖЏЃЎЕБtЮЊКЮжЕЪБЃЌжБЯпPQАбЁїABCЕФжмГЄЗжГЩЯрЕШЕФСНВПЗжЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌЁїABCжаЃЌЁЯABC=45ЁуЃЌAHЁЭBCгкЕуHЃЌЕуDдкAHЩЯЃЌЧвDH=CHЃЌСЌНсBDЃЎ
ЃЈ1ЃЉЧѓжЄЃКBD=ACЃЛ
ЃЈ2ЃЉНЋЁїBHDШЦЕуHа§зЊЃЌЕУЕНЁїEHFЃЈЕуBЃЌDЗжБ№гыЕуEЃЌFЖдгІЃЉЃЌСЌНгAEЃЎ
ЂйШчЭМЂкЃЌЕБЕуFТфдкACЩЯЪБЃЌЃЈFВЛгыCжиКЯЃЉЃЌШєBC=4ЃЌtanC=3ЃЌЧѓAEЕФГЄЃЛ
ЂкШчЭМЂлЃЌЕБЁїEHFЪЧгЩЁїBHDШЦЕуHФцЪБеыа§зЊ30ЁуЕУЕНЪБЃЌЩшЩфЯпCFгыAEЯрНЛгкЕуGЃЌСЌНгGHЃЌЪдЬНОПЯпЖЮGHгыEFжЎМфТњзуЕФЕШСПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCжаЃЌAB=15ЃЌAC=13ЃЌИпAD=12ЃЌдђЁїABCЕФУцЛ§ЮЊ______________ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЂХШчЙћЕШбќШ§НЧаЮСНБпГЄЪЧ6КЭ3ЃЌФЧУДЫќЕФжмГЄЪЧ_______ЃЛ ЂЦвбжЊЕШбќШ§НЧаЮЕФвЛИіЭтНЧЕШгк![]() ЃЌдђЫќЕФЖЅНЧЖШЪ§ЮЊ_______ЃЎ
ЃЌдђЫќЕФЖЅНЧЖШЪ§ЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыШЮаДвЛИіГЩжааФЖдГЦЭМаЮЕФККзжЁЂзжФИЛђЪ§зж______ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com