
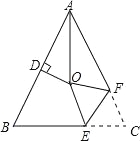
【题目】如图,△ABC中,AB=AC,∠BAC=54°,点D为AB中点,且OD⊥AB,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.
【答案】108
【解析】
试题分析:连接OB、OC,根据角平分线的定义求出∠BAO,根据等腰三角形两底角相等求出∠ABC,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB,根据等边对等角可得∠ABO=∠BAO,再求出∠OBC,然后判断出点O是△ABC的外心,根据三角形外心的性质可得OB=OC,再根据等边对等角求出∠OCB=∠OBC,根据翻折的性质可得OE=CE,然后根据等边对等角求出∠COE,再利用三角形的内角和定理列式计算即可得解.如图,连接OB、OC,∵∠BAC=54°,AO为∠BAC的平分线, ∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×54°=27°,
×54°=27°,
又∵AB=AC, ∴∠ABC=![]() (180°﹣∠BAC)=
(180°﹣∠BAC)=![]() (180°﹣54°)=63°,
(180°﹣54°)=63°,
∵DO是AB的垂直平分线, ∴OA=OB, ∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC﹣∠ABO=63°﹣27°=36°, ∵AO为∠BAC的平分线,AB=AC,
∴△AOB≌△AOC(SAS), ∴OB=OC, ∴点O在BC的垂直平分线上,
又∵DO是AB的垂直平分线, ∴点O是△ABC的外心, ∴∠OCB=∠OBC=36°,
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合, ∴OE=CE,∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°﹣∠COE﹣∠OCB=180°﹣36°﹣36°=108°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
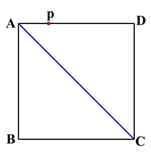
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.则其中男生人数比女生人数多( )
A.11人
B.12人
C.3人
D.4人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图所示),
![]()
操作一:(1)折叠纸面,使1表示的点与1表示的点重合,回答一下问题:
①2表示的点与______表示的点重合;②π表示的点与______表示的点重合。
操作二:(2)折叠纸面,使1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数_____表示的点重合;②![]() 表示的点与数_____表示的点重合
表示的点与数_____表示的点重合
操作三:(3)已知在数轴上点A表示的数是a,点A移动5个单位,此时点A表示的数和a是互为相反数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
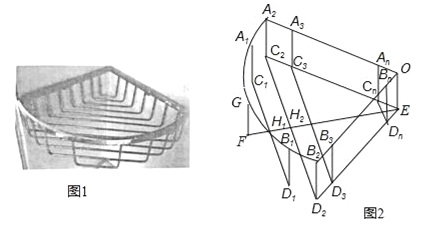
【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在![]() 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
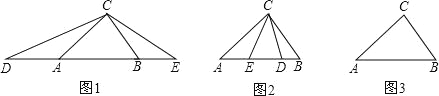
【题目】(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE= ;
(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);
(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
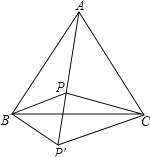
【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com