练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】(1) 定义：直角三角形两直角边的平方和等于斜边的平方．如：直角三角形的直角边分别为3、4，则斜边的平方=32+42=25.已知：Rt△ABC中，∠C=90°，AC=8，AB=10,直接写出BC2=__________________．

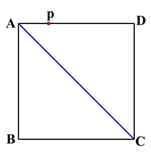
    （2）应用：已知正方形ABCD的边长为4，点P为AD边上的一点，AP= ,请利用“两点之间线段最短”这一原理，在线段AC上画出一点M，使MP+MD最小，并直接写出最小值的平方为_____________．

    【答案】 36 17

    【解析】试题分析：(1)由直角三角形两直角边的平方和等于斜边的平方变形计算得出；

    （2）

    试题解析：

    （1）BC2＝AB2－AC2＝100－64＝36，

    （2）如图所示：作点P关于AC的对称点P’,连接P’D交AC于点M，则点M即为所求，此时有MP+MD最小值，即为P’D的长度.

    过点P’作P’E CD于点E，

    ∵正方形ABCD的边长为4，点P为AD边上的一点，AP=

    ∴P’E＝4，DE＝A P’=AP=1

    ∴DP’2=DE2+P’E2=16+1=17.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，AC的垂直平分线分别交AB、AC于点D、E．

    （1）若∠A = 40°，求∠DCB的度数．

    （2）若AE=4，△DCB的周长为13，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解参加某运动会的2 000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下面说法正确的是( )
    A.2 000名运动员是总体
    B.每个运动员是个体
    C.100名运动员是抽取的一个样本
    D.100名运动员的年龄是抽取的一个样本

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若线段AB＝4，AB∥x轴，点A的坐标是（2，3），则点B的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

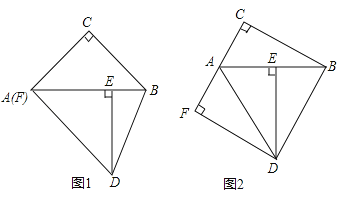
    【题目】在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．

    （1）如图1，若点F与点A重合，求证：AC=BC；

    （2）若∠DAF=∠DBA，①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；

    ②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若等腰△ABC的周长为20，AB=8，则该等腰三角形的腰长为（ ）．

    A.8B.6C.4D.8或6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

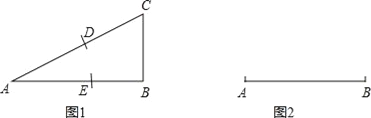
    【题目】（1）如图1，Rt△ABC中，∠B=90°，AB=2BC，现以C为圆心、CB长为半径画弧交边AC于D，再以A为圆心、AD为半径画弧交边AB于E．求证： ．（这个比值叫做AE与AB的黄金比．）

    （2）如果一等腰三角形的底边与腰的比等于黄金比，那么这个等腰三角形就叫做黄金三角形．请你以图2中的线段AB为腰，用直尺和圆规，作一个黄金三角形ABC．

    （注：直尺没有刻度！作图不要求写作法，但要求保留作图痕迹，并对作图中涉及到的点用字母进行标注）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

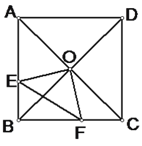
    【题目】在正方形ABCD中，O是对角线的交点，过O作OE⊥OF，分别交AB、BC于E、F，若AE＝4，CF＝3，

    （1）求证：OE=OF

    （2）求 EF的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

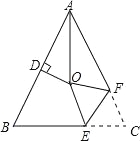
    【题目】如图，△ABC中，AB=AC，∠BAC=54°，点D为AB中点，且OD⊥AB，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为 度．

    查看答案和解析>>

    同步练习册答案