
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A = 40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.

【答案】(1)30°(2)21
【解析】试题分析:(1)由在△ABC中,AB=AC,∠A=40°,根据等腰三角形的性质,可求得∠ACB的度数,又由线段垂直平分线的性质,可得AD=CD,即可求得∠ACD的度数,继而求得答案;
(2)由AE=4,△DCB的周长为13,即可求得△ABC的周长.
试题解析:
(1)在△ABC中 ∵AB=AC ,∠A=40°
∴∠ABC =∠ACB=![]() =70°,
=70°,
∵DE垂直平分AC,
∴DA=DC,
∴在△DAC中,∠DCA=∠A=40°,
∴∠DCB=∠ACB-∠ACD=70°-40°=30°,
(2)∵DE垂直平分AC,
∴DA=DC,EC=EA=4,
∴AC=2AE=8,
C△ABC=AC+BC+BD+DA=8+BC+BD+DC=8+C△CBD=8+13=21.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”.
【探究证明】
(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形;
(2)如图2,求证:∠OAB=∠OAE′.
【归纳猜想】
(3)图1、图2中的“叠弦角”的度数分别为 , ;
(4)图n中,“叠弦三角形” 等边三角形(填“是”或“不是”)
(5)图n中,“叠弦角”的度数为 (用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)
(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
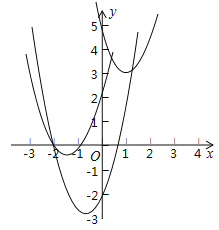
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个图形绕着某一点旋转,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或,这个点叫做它们的.这两个图形在旋转后能重合的对应点叫做关于对称中心的.
查看答案和解析>>
科目:初中数学 来源: 题型:
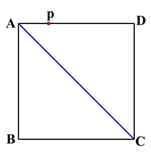
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com