
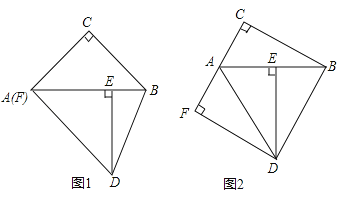
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
【答案】(1)证明见解析;(2)①AF=BE;②AF=![]() x.
x.
【解析】
试题分析:(1)由旋转得到∠BAC=∠BAD,而DF⊥AC,从而得出∠ABC=45°,最后判断出△ABC是等腰直角三角形;
(2)①由旋转得到∠BAC=∠BAD,再根据∠DAF=∠DBA,从而求出∠FAD=∠BAC=∠BAD=60°,最后判定△AFD≌△BED,即可;
②根据题意画出图形,先求出角度,得到△ABD是顶角为36°的等腰三角形,再用相似求出,![]() =
=![]() ,最后判断出△AFD∽△BED,代入即可.
,最后判断出△AFD∽△BED,代入即可.
试题解析:(1)由旋转得,∠BAC=∠BAD,∵DF⊥AC,∴∠CAD=90°,∴∠BAC=∠BAD=45°,∵∠ACB=90°,∴∠ABC=45°,∴AC=CB;
(2)①由旋转得,AD=AB,∴∠ABD=∠ADB,∵∠DAF=∠ABD,∴∠DAF=∠ADB,∴AF∥BB,∴∠BAC=∠ABD,∵∠ABD=∠FAD
由旋转得,∠BAC=∠BAD,∴∠FAD=∠BAC=∠BAD=![]() ×180°=60°,由旋转得,AB=AD,∴△ABD是等边三角形,∴AD=BD,在△AFD和△BED中,∵∠F=∠BED,∠FAD=∠BED,AD=BD,∴△AFD≌△BED,∴AF=BE;
×180°=60°,由旋转得,AB=AD,∴△ABD是等边三角形,∴AD=BD,在△AFD和△BED中,∵∠F=∠BED,∠FAD=∠BED,AD=BD,∴△AFD≌△BED,∴AF=BE;
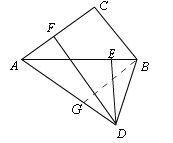
②如图,由旋转得,∠BAC=∠BAD,∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD,由旋转得,AD=AB,∴∠ABD=∠ADB=2∠BAD,∵∠BAD+∠ABD+∠ADB=180°,∴∠BAD+2∠BAD+2∠BAD=180°,∴∠BAD=36°,设BD=x,作BG平分∠ABD,∴∠BAD=∠GBD=36°,∴AG=BG=BC=x,∴DG=AD﹣AG=AD﹣BG=AD﹣BD,∵∠BDG=∠ADB,∴△BDG∽△ADB,∴![]() ,∴
,∴![]() ,∴
,∴![]() =
=![]() ,∵∠FAD=∠EBD,∠AFD=∠BED,∴△AFD∽△BED,∴
,∵∠FAD=∠EBD,∠AFD=∠BED,∴△AFD∽△BED,∴![]() ,∴AF=
,∴AF=![]() =
=![]() x.
x.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】五个新篮球的质量(单位:克)分别是+5、﹣3.5、+0.7、﹣2.5、﹣0.6,正数表示超过标准质量的克数,负数表示不足标准质量的克数.仅从轻重的角度看,最接近标准的篮球的质量是( )
A. ﹣2.5B. ﹣0.6C. +0.7D. +5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
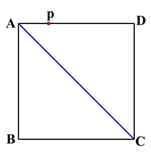
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】拒绝“餐桌浪费”,刻不容缓.节约一粒米的帐:一个人一日三餐少浪费一粒米,全国一年就可以节省3240万斤,这些粮食可供9万人吃一年.“3240万”这个数据用科学记数法表示为( )
A. 0.324×108 B. 32.4×106 C. 3.24×107 D. 324×108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com