
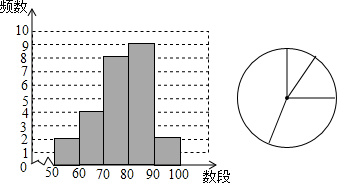
分析 (1)根据频数分布直方图得到80≤x<90范围的人数最多;
(2)用60≤x<70的人数除以总人数得到该组所占的百分比,然后用圆的面积乘以这个百分比即可得到成绩在60≤x<70的人数对应的扇形面积;
(3)先画出树状图展示所有12种等可能的结果数,再找出有C的结果数,然后根据概率公式求解.
解答 解:(1)成绩x在80≤x<90范围的人数最多,有9人;
(2)成绩在60≤x<70的人数对应的扇形面积=$\frac{4}{25}$×π•22=$\frac{16}{25}$π;
(3)50≤x<60的两名同学用A、B表示,90≤x<100的两名同学用C、D表示(小李用C表示),
画树状图为: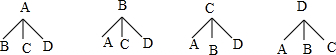
共有12种等可能的结果数,其中有C的结果数为6,
所以小李被选中的概率=$\frac{1}{2}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了扇形统计图和频率分布直方图.


科目:初中数学 来源: 题型:选择题
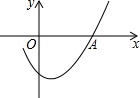 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )| A. | b2<4ac | B. | ac>0 | C. | 2a-b=0 | D. | a-b+c=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①④ | C. | ②④ | D. | ② |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 环数(甲) | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 1 | 1 | 1 | 1 |
| 环数(乙) | 6 | 7 | 8 | 9 | 10 |
| 次数 | 0 | 2 | 2 | 0 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y<0 | B. | y≤0 | C. | y>m | D. | y≥m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
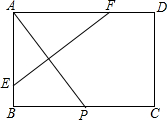 如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.
如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com