
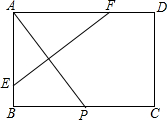
 如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.
如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.分析 (1)在Rt△ABP中,由勾股定理可知AP=5,由折叠的性质可知:AG⊥EF,AG=GP=2.5,设EP=x,则BE=4-x,
在Rt△EBP中,由勾股定理解得:x=$\frac{25}{8}$,在Rt△EGP中,EG=$\sqrt{E{P}^{2}-G{P}^{2}}$=$\frac{15}{8}$,然后再证明△PEG∽△FPE,故此$\frac{EG}{EP}=\frac{EP}{EF}$,从而可求得EF=$\frac{125}{24}$;
(2)如图①所示:首先证明△ABP∽△FAE,可求得AE=$\frac{3}{2}x$,然后在Rt△BEP中,由勾股定理求得:${x}_{1}=6-2\sqrt{5}$,${x}_{2}=6+2\sqrt{5}$;如图②,由折叠的性质可知:BP=AB=4,从而可得到6-$2\sqrt{5}$≤x≤4.
解答 解:(1)如图连接EP、PF.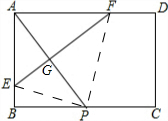
∵点P是BC的中点,
∴PB=3.
在Rt△ABP中,AP=$\sqrt{A{B}^{2}+B{P}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
由折叠的性质可知:AG⊥EF,AG=GP=2.5,∠EAF=∠EPF=90°.
设EP=x,则BE=4-x,
在Rt△EBP中,EP2=EB2+BP2,即:x2=32+(4-x)2,解得:x=$\frac{25}{8}$,
在Rt△EGP中,EG=$\sqrt{E{P}^{2}-G{P}^{2}}$=$\frac{15}{8}$,
∵∠GEP=∠FEP,∠PEG=∠EPF,
∴△PEG∽△FPE.
∴$\frac{EG}{EP}=\frac{EP}{EF}$,即$\frac{\frac{15}{8}}{\frac{25}{8}}=\frac{\frac{25}{8}}{EF}$,
∴EF=$\frac{125}{24}$
(2)如图①所示: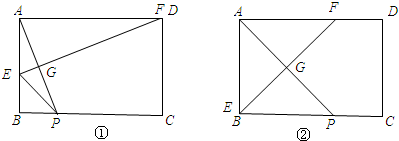
∵∠AEF=∠AEG,∠AGE=∠EAF=90°,
∴∠EAG=∠EFA.
又∵∠ABC=∠DAE.
∴△ABP∽△FAE.
∴$\frac{AF}{AB}=\frac{AE}{BP}$,即$\frac{6}{4}=\frac{AE}{x}$.
∴AE=$\frac{3}{2}x$.
在Rt△BEP中,EP2=BE2+PB2,即:$(4-\frac{3}{2}x)^{2}+{x}^{2}=(\frac{3}{2}x)^{2}$
解得:${x}_{1}=6-2\sqrt{5}$,${x}_{2}=6+2\sqrt{5}$(舍去).
如图②,由折叠的性质可知:BP=AB=4.
∴6-$2\sqrt{5}$≤x≤4.
故答案为:(1)$\frac{125}{24}$;(2)6-$2\sqrt{5}$≤x≤4.
点评 本题主要考查得是相似三角形、勾股定理和翻折变换的综合应用,根据题意画出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
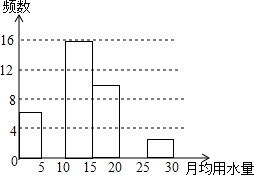 八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | a | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | b |
| 25<x≤30 | 2 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -10 | -4 | 0 | 2 | 2 | … |
| A. | 抛物线的对称轴为x=$\frac{1}{2}$ | |
| B. | 抛物线与x轴的另一个交点为(2,0) | |
| C. | 抛物线与直线y=2的两个交点之间的距离为1 | |
| D. | 在对称轴右侧,y随x增大而增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com