
【题目】近似数8.090精确程度是( )
A. 精确到百分位 B. 精确到万分位 C. 精确到0.001 D. 精确到0.0001
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】定义:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
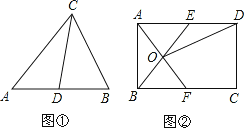
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,AB为直径,点D是弧AC上的一点,连接AD、BD,AC交BD于点F,DE⊥AB于点E,交AC于点P,∠ABD=∠CBD=∠CAD.
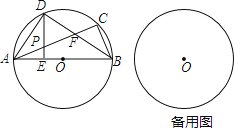
(1)求证:PA=PD;
(2)判断AP与PF是否相等,并说明理由;
(3)当点C为半圆弧的中点,小李通过操作发现BF=2AD,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出BF与AD正确的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (2016广西桂林第7题)下列计算正确的是( )
A.(xy)3=xy3 B.x5÷x5=x C.3x25x3=15x5 D.5x2y3+2x2y3=10x4y9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(![]() )、面数(
)、面数(![]() )、棱数(
)、棱数(![]() )之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题:
)之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题:
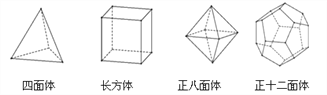
(1)根据上面多面体模型,完成表格中的空格;
多面体 | 顶点数( | 面数( | 棱数( |
四面体 |
|
| |
长方体 |
|
|
|
正八面体 |
|
| |
正十二面体 |
|
|
|
(1)你发现顶点数(![]() )、面数(
)、面数(![]() )、棱数(
)、棱数(![]() )之间存在的关系式是_______.
)之间存在的关系式是_______.
(2)正十二面体有![]() 个顶点,那它有______条棱;
个顶点,那它有______条棱;
(3)一个多面体的面数比顶点数大![]() ,且有
,且有![]() 条棱,则这多面体的顶点数是______;
条棱,则这多面体的顶点数是______;
(4)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有![]() 个顶点,每个顶点处都有
个顶点,每个顶点处都有![]() 条棱,设该多面体表面三角形的个数为
条棱,设该多面体表面三角形的个数为![]() 个,八边形的个数为
个,八边形的个数为![]() 个,求
个,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
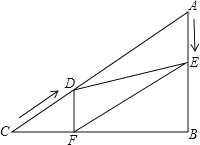
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com