
分析 设汽车的速度是x千米每小时,拖拉机速度y千米每小时,根据甲乙两地相距160千米,1$\frac{1}{3}$小时后相遇和拖拉机继续前进,汽车在相遇处停留1小时后原速返回,在汽车再次出发半小时后追上了拖拉机,列出方程,求出x,y的值,再根据路程=速度×时间即可得出答案.
解答 解:设汽车的速度是x千米每小时,拖拉机速度y千米每小时,根据题意得:
$\left\{\begin{array}{l}{\frac{4}{3}(x+y)=160}\\{\frac{1}{2}x=\frac{3}{2}y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=90}\\{y=30}\end{array}\right.$,
则汽车汽车行驶的路程是:($\frac{4}{3}$+$\frac{1}{2}$)×90=165(千米),
拖拉机行驶的路程是:($\frac{4}{3}$+$\frac{3}{2}$)×30=85(千米).
答:汽车行驶165千米,拖拉机形式85千米.
点评 本题主要考查了二元一次方程组的应用的知识点,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键;本题用到的知识点是路程=速度×时间.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
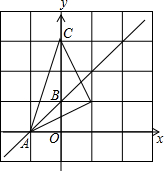 如图,若△A′B′C′与△ABC关于直线AB对称,则点C的对称点C′的坐标是( )
如图,若△A′B′C′与△ABC关于直线AB对称,则点C的对称点C′的坐标是( )| A. | (0,1) | B. | (0,-3) | C. | (3,0) | D. | (2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
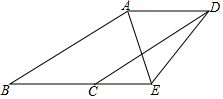 已知如图,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,当∠ADC:∠CDE=3:2,且∠AED=60°时,求∠BED的度数为$\frac{960}{7}$度.
已知如图,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,当∠ADC:∠CDE=3:2,且∠AED=60°时,求∠BED的度数为$\frac{960}{7}$度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
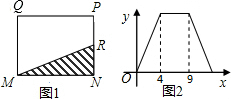
| A. | M处 | B. | N处 | C. | P处 | D. | Q处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
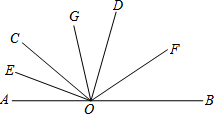 如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.
如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com