
【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.

(1)若AB//x轴,如图一,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合) , 使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标;
(3)设点A关于x轴的对称点为 ![]() ,连接
,连接 ![]() ,在点P运动的过程中,∠
,在点P运动的过程中,∠ ![]() 的度数是否会发生变化,若不变,请求出∠
的度数是否会发生变化,若不变,请求出∠ ![]() 的度数,若改变,请说明理由。
的度数,若改变,请说明理由。
【答案】
(1)解:过点B作BC⊥x轴于点C,如图1所示.
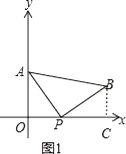
∵AO⊥x轴,BC⊥x轴,且AB//x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°﹣∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
t=4÷1=4(秒),
故t的值为4
(2)解:点M的坐标为(4,7), (6,-4), (10,-1)
(3)解: ![]()
∵△APB为等腰直角三角形,
∴∠APO+∠BPC=180°﹣90°=90°.
又∵∠PAO+∠APO=90°,
∴∠PAO=∠BPC.
在△PAO和△BPC中, 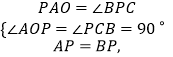
∴△PAO≌△BPC,
∴AO=PC,BC=PO.
∵点A(0,4),点P(t,0)
∴PC=AO=4,BC=PO=t,CO=PC+PO=4+ t
∴点 ![]()
∴过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() ,
,
![]()
![]() 为等腰直角三角形.
为等腰直角三角形.
∴∠ ![]() =45°
=45°
【解析】 (1)过点B作BC⊥x轴于点C,如图1所示.根据题意首先判断出四边形ABCO为长方形,然后根据矩形的性质得出AO=BC,根据等腰直角三角形的性质知AP=BP,∠PAB=∠PBA=45°,从而得出∠OAP=45°,进而判断出△AOP为等腰直角三角形,根据等腰直角三角形的性质得出OA=OP=4,然后根据时间=路程除以速度算出结果;
(2)当t=3时OP=3,又OA=4,根据勾股定理得出AP的长,根据等腰直角三角形的意义得出AP=BP,再根据勾股定理得出AB的长,然后分类讨论当△MPB和△ABP全等时,易得点M的坐标为(4,7), (10,-1);当△MPB与△APB全等时,此时点M与点A关于点P 对称易得点M的坐标为(6,-4), 综上所述从而得出答案;
(3) 根据等腰直角三角形的性质及同角的余角相等得出∠PAO=∠BPC,然后利用SAS判断出△PAO≌△BPC,根据全等三角形对应边相等得出AO=PC,BC=PO,根据A,P两点的坐标表示出PC=AO=4,BC=PO=t,CO=PC+PO=4+ t,从而得出b点的坐标,过点 B 作 B H ⊥ y 轴于点 H ,BH=OC=4+t=A′H,判断出△ A ′ H B 为等腰直角三角形,得出结论。
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°).


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 . 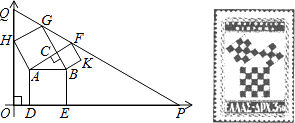
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国流传了上千年的传统节日,全国各地举行了丰富多彩的纪念活动,为了继承传统,减缓学生考前的心理压力,某班学生组织了一次拔河比赛,裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置,规则是:石头胜剪刀,剪刀胜布,布胜石头,手势相同则再决胜负.
(1)用列表或画树状图法,列出甲、乙两队手势可能出现的情况;
(2)裁判员的这种做法对甲、乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为真命题的是( )
A.和为180°的两个角是邻补角B.内错角相等
C.经过直线外一点有且只有一条直线与这条直线平行D.同旁内角相等,两直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com