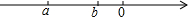Question

10．a，b两数在数轴上的位置如图所示，M=a+b，N=-a+b，H=a-b，G=-a-b，则下列正确的是（　　）

• A． G＞H＞M＞N
• B． G＞N＞M＞H
• C． G＞M＞N＞H
• D． G＞N＞H＞M

Answer 1

分析 根据数轴得出a＜0，b＜0，-a＞-b，判断出M=a+b＜0，N=-a+b＞0，H=a-b＜0，G=-a-b＞0，再根据a+b＜a-b，-a+b＜-a-b，即可得出答案．

解答 解：∵从数轴可知：a＜0，b＜0，-a＞-b，
∴M=a+b＜0，
N=-a+b＞0，
H=a-b＜0，
G=-a-b＞0，
∵a+b＜a-b，-a+b＜-a-b，
∴M＜H，N＜G，
∴G＞N＞H＞M，
故选：D．

点评 此题考查了数轴与有理数的大小比较，由于引进了数轴，我们把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．