Question

【题目】（1）如图1，直线a∥b∥c∥d，且a与b，c与d之间的距离均为1，b与c之间的距离为2，现将正方形ABCD如图放置，使其四个顶点分别在四条直线上，求正方形的边长；
（2）在（1）的条件下，探究：将正方形ABCD改为菱形ABCD，如图2，当∠DCB=120°时，求菱形的边长．

Answer 1

【答案】解：（1）如图1，过B，D分别作直线d的垂线，垂足分别为P，Q，
∵四边形ABCD是正方形，
∴AB=BC=CD=DA，∠BCD=90°，
∴∠PCB+∠QCD=90°，
∵∠PBC+∠PCB=90°，
∴∠PBC=∠QCD，
在△CBP和△CDQ中

∴△CBP≌△CDQ（AAS），
∴CP=DQ=1，
∵BP=3，
∴；
（2）如图2，过B，D分别作直线d的垂线，垂足分别为M，N，作∠BPC=∠DQC=120°，P，Q在直线d上，
∵∠DCB=120°，
∴∠PCB+∠DCQ=60°，
∵∠PBC+∠PCB=60°，
∴∠PBC=∠DCQ，
在△BPC和△CQD中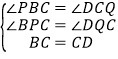

∴△BPC≌△DQC，
∴PC=DQ，PB=CQ，
∵∠BPC=∠DQC=120°，
∴∠BPM=∠DQN=60°，
∴sin∠BPM=，sin∠DQN=，
∵BM=3，DN=1，
∴PB=2，DQ=，
∴PC=DQ=，
∵∠BPM=60°，
∴∠PBM=30°，
∵在RT△PBM中，PM=PB=，
∴MC=PC+PM=，
∴在RT△PBM中，BC===．

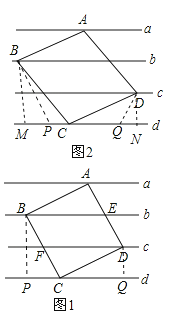
【解析】（1）如图1，过B，D分别作直线d的垂线，垂足分别为P，Q，通过证得△CBP≌△CDQ，得出CP=DQ=1，然后根据勾股定理即可求得；
（2）如图2，过B，D分别作直线d的垂线，垂足分别为M，N，作∠BPC=∠DQC=120°，P，Q在直线d上，通过证得△BPC≌△DQC证得PC=DQ，通过解直角三角形求得PM，DQ，进而求得MC，然后根据勾股定理即可求得．
【考点精析】关于本题考查的正方形的性质，需要了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案．