【题目】如图，将平行四边形ABCD折叠，使顶点D恰好落在AB边上的点M处，折痕为AN，有以下四个结论①MN∥BC；②MN=AM；③四边形MNCB是矩形；④四边形MADN是菱形，以上结论中，你认为正确的有_____________（填序号）．
【答案】①②④
【解析】
根据四边形ABCD是平行四边形，可得∠B=∠D，再根据折叠可得∠D=∠NMA，再利用等量代换可得∠B=∠NMA，然后根据平行线的判定方法可得MN∥BC；证明四边形AMND是平行四边形，再根据折叠可得AM=DA，进而可证出四边形AMND为菱形，再根据菱形的性质可得MN=AM，不能得出∠B=90°；即可得出结论．
解：∵四边形ABCD是平行四边形，
∴∠B=∠D，
∵根据折叠可得∠D=∠NMA，
∴∠B=∠NMA，
∴MN∥BC；①正确；
∵四边形ABCD是平行四边形，
∴DN∥AM，AD∥BC，
∵MN∥BC，
∴AD∥MN，
∴四边形AMND是平行四边形，
根据折叠可得AM=DA，
∴四边形AMND为菱形，
∴MN=AM；②④正确；
没有条件证出∠B=90°，④错误；
故答案为：①②④．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】为了更好治理西太湖水质，保护环境，市治污公司决定购买10 台污水处理设备，现有A、B两种型号的设备，其中每台的价格，月处理污水量如下表:
经调查:购买-台A型设备比购买一-台B型设备多2万元，购买2台A型设备比购买4台B型设备少4万元.
(1)求a、b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过47万元，并且该月要求处理西太湖的污水量不低于1860 吨，则有哪几种购买方案?请指出最省钱的一种购买方案，并指出相应的费用.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点
是坐标原点，
，
，
均为等边三角形，
在
轴正半轴上，点
，点
，点
在内部，点
在的外部，
，
，
与
交于点
，连接
，
，
，
.
（1）求点的坐标；
（2）判断与的数量关系，并说明理由；
（3）直接写出
的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在表盘上12：00时，时针、分针都指向数字12，我们将这一位置称为“标准位置”(图中
)．小文同学为研究12点
分(
)时，时针与分针的指针位置，将时针记为
，分针记为
．如：12：30时，时针、分针的位置如图2所示，试解决下列问题：
（1）分针每分钟转动 °；时针每分钟转动 °；
（2）当与在同一直线上时，求的值；
（3）当、、两两所夹的三个角
、
、
中有两个角相等时，试求出所有符合条件的的值．(本小题中所有角的度数均不超过180°)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某汽车交易市场为了解二手轿车的交易情况，将本市场去年成交的二手轿车的全部数据，以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类，并根据这些数据由甲，乙两人分别绘制了下面的两幅统计图（图都不完整）．
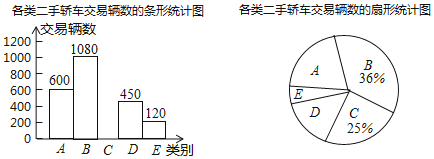
请根据以上信息，解答下列问题：
（1）该汽车交易市场去年共交易二手轿车 辆．
（2）把这幅条形统计图补充完整．（画图后请标注相应的数据）
（3）在扇形统计图中，D类二手轿车交易辆数所对应扇形的圆心角为 度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为（ ）
A. 6 B. 4
C. 3 D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．
（1）求证：AF=DC ；
（2）若∠BAC=
，试判断四边形ADCF的形状，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
