
 ��ͼ����֪��������x�ύ��A��-1��0����B��5��0�����㣬��y�ύ�ڵ�C��0��5����
��ͼ����֪��������x�ύ��A��-1��0����B��5��0�����㣬��y�ύ�ڵ�C��0��5�������� ��1������������x�����������������������ߵĽ���ʽΪy=a��x+1����x-5��������C��0��3�����������߽���ʽ�м��ɵó�����aһԪһ�η��̣��ⷽ�̼������a��ֵ���Ӷ��ó������ߵĽ���ʽ��
��2������ֱ��BC�ĺ�������ʽΪy=kx+b����ϵ�B����C�����꣬���ô���ϵ�������ֱ��BC�ĺ�������ʽ�����ɵ�D������Ϊm�ó���D����E�����꣬��������ľ��빫ʽ�Լ������ε������ʽ�����ɵó����ۣ����ɢٵĽ��ۣ������䷽����S����m�ĺ�����ϵʽ���б��Σ��Ӷ��ó����ۣ��۽��ͼ���֪��BDE�͡�BFE�ǵȸߵģ��ɴ˵ó����ǵ������=DE��EF��������������ǣ����������ľ��빫ʽ���ɵó�����m�ķ�ʽ���̣��ⷽ�̼��ɵó�m��ֵ��������뵽��D�������м��ɵó����ۣ�
��� ��1���������߾���A��-1��0����B��5��0����C��0��5����
����y=a��x+1����x-5����
��5=a��0+1����0-5����
���a=-1��
�������ߵĺ�����ϵʽΪy=-��x+1����x-5����
��y=-x2+4x+5��
��2������ֱ��BC�ĺ�����ϵʽΪy=kx+b����
$\left\{\begin{array}{l}b=5\\ 5k+b=0.\end{array}\right.$
���$\left\{\begin{array}{l}k=-1\\ b=5.\end{array}\right.$��
��y=-x+5��
��D��m��-m2+4m+5����E��m��-m+5����
��DE=-m2+4m+5+m-5=-m2+5m
��s=$\frac{1}{2}��5$��-m2+5m��=-$\frac{5}{2}$m2+$\frac{25}{2}$m ��0��m��5����
��s=-$\frac{5}{2}$m2+$\frac{25}{2}$m=$-\frac{5}{2}{��{m-\frac{5}{2}}��^2}+\frac{125}{8}$��
��$-\frac{5}{2}��0$��
�൱m=$\frac{5}{2}$ʱ��S�����ֵ��S���ֵ=$\frac{125}{8}$��
�ۡߡ�BDE�͡�BFE�ǵȸߵģ�
�����ǵ������=DE��EF��
��������DE��EF=2��3ʱ��
��$\frac{{-{m^2}+5m}}{-m+5}=\frac{2}{3}$��
��ã�${m_1}=\frac{2}{3}��{m_2}=5$���ᣩ��
��ʱ��D��$\frac{2}{3}��\frac{65}{9}$����
��������DE��EF=3��2ʱ��
��$\frac{{-{m^2}+5m}}{-m+5}=\frac{3}{2}$��
��ã�${m_1}=\frac{3}{2}��{m_2}=5$���ᣩ��
��ʱ��D��$\frac{3}{2}��\frac{35}{4}$����
������������D��������$\frac{2}{3}��\frac{65}{9}$����$\frac{3}{2}��\frac{35}{4}$����
���� �������ڶ��κ����ۺ��⣬��Ҫ�����˶��κ��������ʡ�����ϵ������������ʽ�������ľ��빫ʽ�Լ������ε������ʽ���ۺ�Ӧ�ã�����Ĺؼ������ô���ϵ������������ʽ���ҳ�ֱ��BC�ĺ�������ʽ�������䷽�������ֵ���⣮����ʱע���������˼������ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=��x-2��2 | B�� | y=��x+2��2 | C�� | y=x2-2 | D�� | y=x2+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
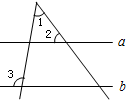 ��ͼ��ֱ��a��b������2=55�㣬��3=100�㣬���1�Ķ���Ϊ��������
��ͼ��ֱ��a��b������2=55�㣬��3=100�㣬���1�Ķ���Ϊ��������| A�� | 35�� | B�� | 45�� | C�� | 50�� | D�� | 55�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
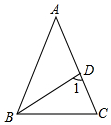 ��ͼ���ڡ�ABC�У�AB=AC����BAC=36�㣬BDƽ�֡�ABC�����1�Ķ�����72�㣮
��ͼ���ڡ�ABC�У�AB=AC����BAC=36�㣬BDƽ�֡�ABC�����1�Ķ�����72�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
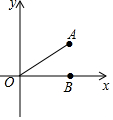 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��A��4��3���͵�B��4��0������sin��AOB��ֵ���ڣ�������
��ͼ����ƽ��ֱ������ϵxOy�У���֪��A��4��3���͵�B��4��0������sin��AOB��ֵ���ڣ�������| A�� | $\frac{3}{4}$ | B�� | $\frac{3}{5}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com