
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
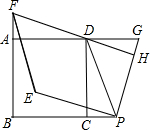 如图已知,四边形ABCD是正方形,点P与点G分别在线段BC与线段AD的延长线上,PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.
如图已知,四边形ABCD是正方形,点P与点G分别在线段BC与线段AD的延长线上,PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
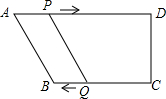 如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,问几秒时,四边形ABQP是平行四边形?
如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,问几秒时,四边形ABQP是平行四边形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
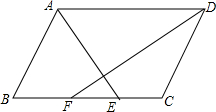 如图,在?ABCD中,AB=4,AD=6,AE、DF分别平分∠BAD、∠ADC,交BC于E、F两点.
如图,在?ABCD中,AB=4,AD=6,AE、DF分别平分∠BAD、∠ADC,交BC于E、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
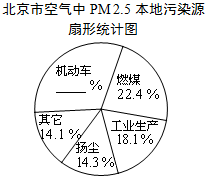 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com