
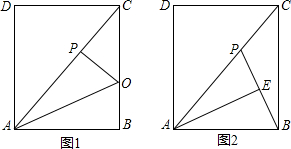
分析 (1)由折叠有:AP=AB,∠ABC=∠APO=90°,由AD∥BC,得到∠DAC=∠ACB,从而判断出△ADC∽△CPO;
(2)利用相似三角形的面积比等于相似比的平方,再利用勾股定理建立方程即可;
(3)利用三角形的相似计算出线段PM=$\frac{24}{5}$,AM=$\frac{18}{5}$,再利用S△ABP=$\frac{1}{2}$AB×PM=$\frac{1}{2}$PB×AE,AE=$\frac{12\sqrt{5}}{5}$,即可.
解答 (1)证明:由折叠有:AP=AB,∠ABC=∠APO=90°,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠CPO=∠D=90°,
∵∠DAC=∠ACB,
∴△ADC∽△CPO
(2)∵△ADC∽△CPO,且$\frac{{S}_{△ADC}}{{S}_{△POC}}$=$\frac{4}{1}$,
∴$\frac{AD}{PC}$=$\frac{2}{1}$,
∴PC=4,设CD=x,
∴AB=AP=x,
∴64+x2=(x+4)2,
∴x=6,
∴CD=6;
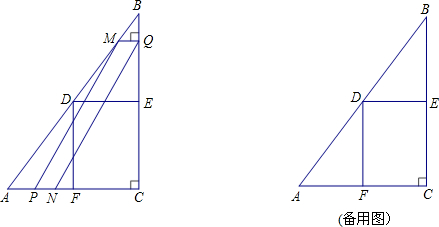
(3)①如图3,
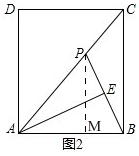
作PM⊥AB(如图2),
∴△APM∽△ACB,
∴PM=$\frac{24}{5}$,AM=$\frac{18}{5}$,
∴BM=$\frac{12}{5}$,
∴PB=$\frac{12\sqrt{5}}{5}$,
∵AP=AB,AE⊥PB,
∴BE=$\frac{6\sqrt{5}}{5}$,
∵S△ABP=$\frac{1}{2}$AB×PM=$\frac{1}{2}$PB×AE,
∴AE=$\frac{12\sqrt{5}}{5}$,
∵四边形BEFE′是正方形,
∴BE=BE′=$\frac{6\sqrt{5}}{5}$,E′F∥PB,
∴$\frac{AG}{AP}=\frac{AE′}{AE}$,
∴AG=3.
②如图4,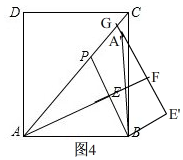
∵四边形BEFE'是正方形,
∴BP∥E'F,
∴$\frac{AG}{AP}=\frac{AF}{AE}$,
∴$\frac{AG}{6}=\frac{\frac{18\sqrt{5}}{5}}{\frac{12\sqrt{5}}{5}}$,
∴AG=9
∴满足条件的AG=3或9.
点评 此题是几何变换综合题,用到的知识点是相似三角形的判定与性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质,关键是做出辅助线,找出全等和相似的三角形.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 10.1×103 | B. | 1.01×104 | C. | 1.01×105 | D. | 0.101×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
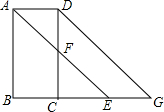 如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB
如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | -3 | -3 |
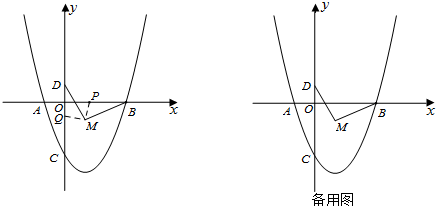
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
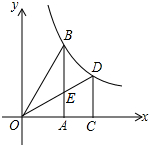 y=$\frac{3\sqrt{2}}{x}$.
y=$\frac{3\sqrt{2}}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com