
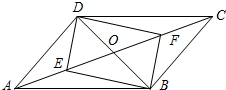
 平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动
平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动分析 (1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;
(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:18-2t-2t=10,继而求得答案.
解答 解:(1)四边形DEBF是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,
∴AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)根据题意得:AE=CF=2tcm或18-2tcm,
∵四边形DEBF是平行四边形,
∴当EF=BD时,四边形DEBF为矩形.
即AC-AE-CF=BD或AE+CF-AC=EF,
∴18-2t-2t=10或2t+2t-18=10,
解得:t=2或t=7
∴当运动时间t为2s或7s时,四边形DEBF为矩形.
点评 此题考查了平行四边形的判定与性质以及矩形的判定,正确应用矩形的判定方法得出EF=BD是解题关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
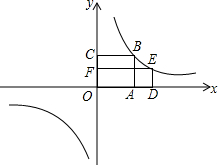 解决问题:
解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 48cm2 | B. | 24cm2 | C. | 18cm2 | D. | 12cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
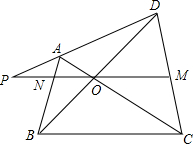 已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.
已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
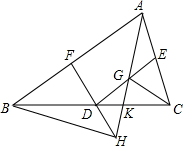 如图,在△ABC中,D、E、F分别是三边BC、AC、AB的中点,连结DE,在DE上任取一个点G,AG的延长线交FD的延长线于H,交CD于K,连结CG.求证:CG∥BH.
如图,在△ABC中,D、E、F分别是三边BC、AC、AB的中点,连结DE,在DE上任取一个点G,AG的延长线交FD的延长线于H,交CD于K,连结CG.求证:CG∥BH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com