
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起.
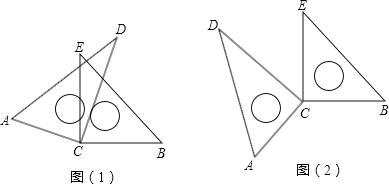
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
【答案】(1)∠ACE=∠BCD;(2)150°;(3)∠ECD+∠ACB=180°;(4)成立.
【解析】解:(1)∠ACE=∠BCD,理由如下:
∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD;
(2)若∠DCE=30°,∠ACD=90°,
∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°;
(3)猜想∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°;
(4)成立.


科目:初中数学 来源: 题型:
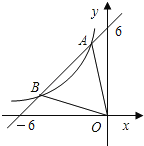
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为原点,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0.
![]()
(1)a=________,b=_________;
(2)若点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(秒).
①当点P运动到线段OB上,且PO=2PB时,求t的值;
②先取OB的中点E,当点P在线段OE上时,再取AP的中点F,试探究![]() 的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.
的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.
③若点P从点A出发,同时,另一动点Q从点B出发,以每秒2个单位长度的速度向左匀速运动,到达点O后立即原速返回向右匀速运动,当PQ=1时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲种铅笔每支0.4元,乙种铅笔每支0.6元,某同学共购买了这两种铅笔30支,并且买乙种铅笔所花的钱是买甲种铅笔所花的钱的3倍.
(1)该同学购买甲乙两种铅笔各多少支?
(2)求该同学购买这两种铅笔共花了多少元钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com