练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线经过点．

    （1）求此抛物线的函数解析式；

    （2）判断点是否在此抛物线上；

    （3）求出抛物线上纵坐标为的点的坐标．

    【答案】（1）y=-2x2；（2）点B（1，4）不在此抛物线上；（3）（-，-6），（，-6）

    【解析】

    （1）把A点代入y=ax2中求出a的值即可；
    （2）根据二次函数图象上点的坐标特征进行判断；
    （3）解方程-2x2=-6即可．

    解：（1）把A（-2，-8）代入y=ax2得4a=-8，解得a=-2，
    ∴此抛物线的函数解析式为y=-2x2；
    （2）当x=1时，y=-2x2=-2，
    ∴点B（1，4）不在此抛物线上；
    （3）当y=-6时，-2x2=-6，
    解得x=±，

    ∴抛物线上纵坐标为-6的点的坐标为（-，-6），（，-6）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

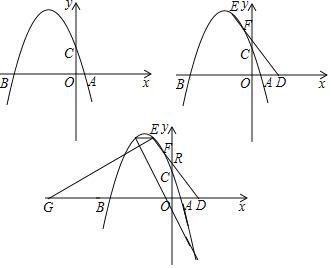
    【题目】抛物线y＝﹣x+c交x轴于A、B两点（B在A左侧），交y轴于C，AB＝10．

    （1）求抛物线的解析式；

    （2）在A点右侧的x轴上取点D，E为抛物线上第二象限内的点，连接DE交抛物线另外一点F，tan∠BDE＝，DF＝2EF，求E点坐标；

    （3）在（2）的条件下，点G在x轴负半轴上，连接EG，EH∥AB交抛物线另外一点H，点K在第四象限的抛物线上，设DE交y轴于R，∠EHK＝∠EGD+∠ORD，当HK＝EG，求K点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在平面直角坐标系内，的三个顶点的分别为，，（正方形网格中每个小正方形的边长是一个单位长度）．

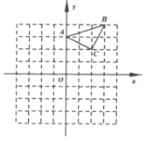
    （1）在网格内画出向下平移2个单位长度得到的，点的坐标是________；

    （2）以点为位似中心，在网格内画出，使与位似，且位似比为，点的坐标是________；

    （3）的面积是________平方单位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在矩形 ABCD 中 AB=8，BC=6，AE=BE，点 F 为边 BC 上任意一点，将BEF 沿着 EF 翻折，点 B 为点 B 的对应点，则当BCD 的面积最小时BCF 的面积为（ ）

    A.4B.6C.4.2D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝﹣x2+x﹣1与x轴交于点A，B(点A在点B的左侧)，与y轴交于点C，其顶点为D．将抛物线位于直线l：y＝t(t＜)上方的部分沿直线l向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．

    (1)点A，B，D的坐标分别为　 　，　 　，　 　；

    (2)如图①，抛物线翻折后，点D落在点E处．当点E在△ABC内(含边界)时，求t的取值范围；

    (3)如图②，当t＝0时，若Q是“M”形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P？若存在，求出点P的坐标；若不存在，请说明理由．

    [Failed to download image : http://192.168.0.10:8086/QBM/2019/5/28/2213337932849152/2214008649842688/STEM/890e59b444e5404588b8511540e03e41.png]

    查看答案和解析>>

    科目：初中数学 来源： 题型：

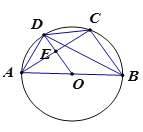
    【题目】如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙D于点D,交AC于点E,连接AD,BD,CD若AB=10,cos∠ABC=,则tan∠DBC的值是( )

    A.B.C.2D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知,点A为⊙0外一点,过A作⊙O的切线与⊙O相切于点P，连接PO并延长至圆上一点B连接AB交⊙O于点C,连接OA交⊙O于点D连接DP且∠OAP=∠DPA。

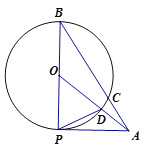
    （1）求证：PO=PD

    (2)若AC=,求⊙O的半径。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

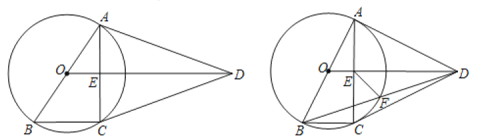
    【题目】如图，四边形ABCD中，AB＝AD＝CD，以AB为直径的⊙O经过点C，连接AC，OD交于点E．

    （1）证明：OD∥BC；

    （2）若AD是⊙O的切线，连接BD交于⊙O于点F，连接EF，且OA＝1，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个盒子中有1个白球和2个红球，这些球除颜色外都相同.

    ⑴如果从盒子中随机摸出1个球，摸出红色球的概率为_____________；

    ⑵若从盒子中随机摸出一个球，记下颜色后放回，再从中随机摸出一个球，请通过列表或画树状图的方法，求两次摸到不同颜色球的概率.

    查看答案和解析>>

    同步练习册答案