
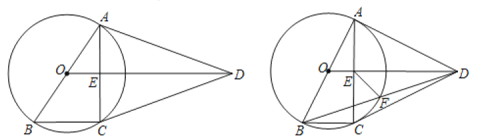
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)证明:OD∥BC;
(2)若AD是⊙O的切线,连接BD交于⊙O于点F,连接EF,且OA=1,求EF的长.
【答案】(1)见解析;(2)EF=![]()
【解析】
(1)连接OC,证明△ADO≌△CDO,根据全等三角形的性质得到∠AOD=∠COD,由圆周角定理可证∠AOD=∠ABC,根据等腰三角形的性质得到∠OBC=∠OCB,根据平行线的判定定理即可得到结论;
(2)连接AF,过F作FM⊥EF交OD于M,推出△ABD为等腰直角三角形,求得∠AFB=90°,∠DAF=∠45°,由△AEF≌△DMF可得AE=DM,由△AOE∽DOA求出AE的长,进而可求EF的长.
解:(1)连接OC,
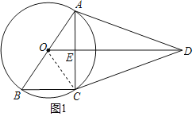
∵AO=CO,AD=CD,OD=OD,
∴△ADO≌△CDO(SSS),
∴∠AOD=∠COD,
∵∠AOC=2∠ABC,
∴∠AOD=∠ABC,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠COD,
∴OD//BC;
(2)连接AF,过F作FM⊥EF交OD于M,
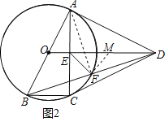
∵AB=AD,AD是圆的切线,
∴△ABD为等腰直角三角形,
∵AB为直径,
∴∠AFD=90°,∠DAF=∠45°,
∵∠AED=∠AFD=90°,
∴∠DAF=∠DEF=45°,
∴AF=DF,
∴∠AFE=∠DFM,
∵∠EAF=∠FDM,
∴△AEF≌△DMF(ASA),
∴AE=DM.
∵OA=1,
∴AD=2,
∴OD=![]() ,
,
∵∠AOE=∠AOD,∠AEO=∠OAD,
∴△AOE∽DOA,
∴![]() ,
,
∴AE=![]() ,
,
∴DM=![]() ,
,
∴DE=![]() ,
,
∴EM=![]() ,
,
∴EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程 (a+2b)x2-2![]() x+
x+![]() (a+2b)=0有实数根.
(a+2b)=0有实数根.
(1)若a=2,b=1,求方程的根
(2)若m=a2+b2+5a,若b<0,求m的取值范围.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
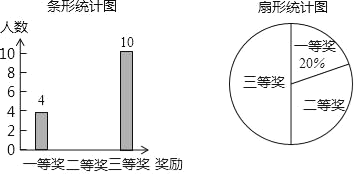
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)如果该校八年级有800人,请你估计获奖的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
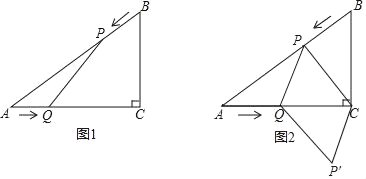
【题目】已知:如图1在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P由点B出发沿BA方向向点A匀速运动,速度为2cm/s;同时点Q由点A出发沿AC方向点C匀速运动,速度为lcm/s;连接PQ,设运动的时间为t秒(0<t<5),解答下列问题:
(1)当为t何值时,PQ∥BC;
(2)设△AQP的面积为y(cm2),求y关于t的函数关系式,并求出y的最大值;
(3)如图2,连接PC,并把△PQC沿QC翻折,得到四边形PQPC,是否存在某时刻t,使四边形PQP'C为菱形?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲地有42吨货物要运到乙地,有大、小两种货车可供选择,具体收费情况如表:
类型 | 载重量(吨) | 运费(元/车) |
大货车 | 8 | 450 |
小货车 | 5 | 300 |
运完这批货物最少要支付运费_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
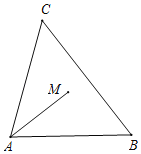
【题目】如图,在△ABC中,AB=AC=5,BC=6,点M在△ABC内,AM平分∠BAC.点E与点M在AC所在直线的两侧,AE⊥AB,AE=BC,点N在AC边上,CN=AM,连接ME,BN.
(1)补全图形;
(2)求ME:BN的值;
(3)问:点M在何处时BM+BN取得最小值?确定此时点M的位置,并求此时BM+BN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
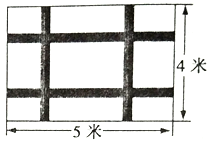
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.
查看答案和解析>>
科目:初中数学 来源: 题型:
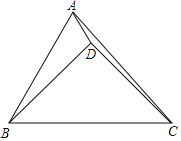
【题目】如图,△ABC中,∠ABC=60°,BC=8,点D为△ABC内一点,BD=CD,∠ABD+∠ADC=180°,若AD=2,则AC的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com