
分析 首先根据x>0,y>0,且x-$\sqrt{xy}$-2y=0,判断出x、y的大小关系,然后求出的x、y的大小关系代入$\frac{{2x-\sqrt{xy}}}{{y+2\sqrt{xy}}}$,求出算式的值是多少即可.
解答 解:∵x-$\sqrt{xy}$-2y=0,
∴($\sqrt{x}$-2$\sqrt{y}$)($\sqrt{x}$$+\sqrt{y}$)=0,
∴$\sqrt{x}$=2$\sqrt{y}$或$\sqrt{x}$=-$\sqrt{y}$,
∵x>0,y>0,
∴$\sqrt{x}$=-$\sqrt{y}$不符合题意,
∴$\sqrt{x}$=2$\sqrt{y}$,x=4y,
∴$\frac{{2x-\sqrt{xy}}}{{y+2\sqrt{xy}}}$=$\frac{2×4y-\sqrt{4y•y}}{y+2\sqrt{4y•y}}$=$\frac{8y-2y}{y+4y}=\frac{6y}{5y}$=$\frac{6}{5}$,
即$\frac{{2x-\sqrt{xy}}}{{y+2\sqrt{xy}}}$的值是$\frac{6}{5}$.
故答案为:$\frac{6}{5}$.
点评 (1)此题主要考查了二次根式的性质和化简,要熟练掌握,解答此类问题的关键是要明确化简二次根式的步骤:①把被开方数分解因式;②利用积的算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2.
(2)解答此题的关键是判断出x、y的大小关系.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
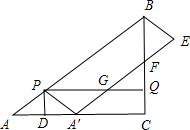 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
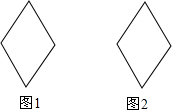 如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.
如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
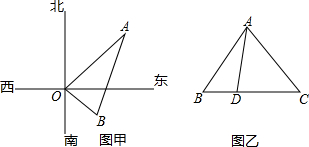
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )
在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )| A. | 16 | B. | 8 | C. | 8$\sqrt{2}$ | D. | 8$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com