
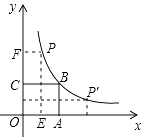
 如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=$\frac{k}{x}$(k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=$\frac{k}{x}$(k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.分析 (1)根据正方形的面积求得B的坐标,利用待定系数法求得反比例函数的解析式;
(2)分成P在B的左侧和右侧两种情况进行讨论.当P在B的左侧时,重合部分是以OC为边的矩形,根据面积公式求得P的横坐标,进而代入反比例函数解析式求得纵坐标;当P在B的右侧时,重合部分是以OA为一边的矩形,根据面积公式求得P的纵坐标,进而求得横坐标;
(3)与(2)的解法相同,分成两种情况进行讨论.
解答 (1)∵正方形OABC的面积为9,∴OA=OC=3,∴B(3,3),
又∵点B(3,3)在函数y=$\frac{k}{x}$的图象上,∴k=9;
(2)分两种情况:①当点P在点B的左侧时,
∵P(m,n)在函数y=$\frac{k}{x}$上,
∴mn=9,
∴S=m(n-3)=mn-3m=$\frac{9}{2}$,解得m=$\frac{3}{2}$,
∴n=6,∴点P的坐标是P($\frac{3}{2}$,6);
②当点P在点B的右侧时,
∵P(m,n)在函数y=$\frac{k}{x}$上,
∴mn=9,
∴S=n(m-3)=mn-3n=$\frac{9}{2}$,
解得n=$\frac{3}{2}$,∴m=6,
∴点P的坐标是P(6,$\frac{3}{2}$),
综上所述:P(6,$\frac{3}{2}$),($\frac{3}{2}$,6).
(3)当0<m<3时,点P在点B的左边,此时S=9-3m,
当m≥3时,点P在点B的右边,此时S=9-3n=9-$\frac{27}{m}$.
点评 本题考查了待定系数法求反比例函数的解析式,以及反比例函数比例系数的几何意义,注意到分情况讨论是关键.


科目:初中数学 来源: 题型:解答题
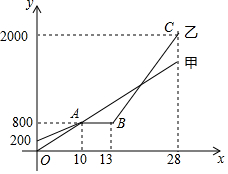 甲、乙相约去离家2000m的公园晨练,甲先出发一直匀速前行,乙后出发,如图是甲和乙所走的路程s(m)与时间t(min)的函数图象.
甲、乙相约去离家2000m的公园晨练,甲先出发一直匀速前行,乙后出发,如图是甲和乙所走的路程s(m)与时间t(min)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
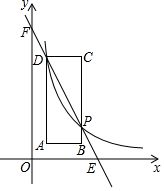 如图,矩形ABCD中,点A(1,1)、B(3,1),C(3,6),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,且与BC交于点P.
如图,矩形ABCD中,点A(1,1)、B(3,1),C(3,6),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,且与BC交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
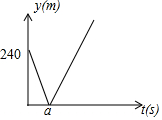 甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.
甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
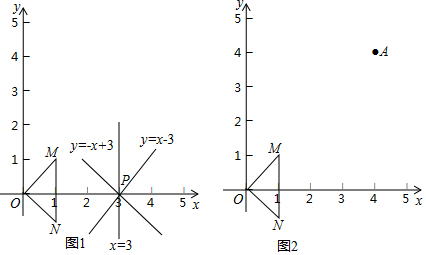
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
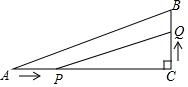 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )| A. | 20cm | B. | 18cm | C. | 2$\sqrt{5}$cm | D. | 3$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
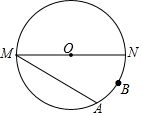 如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.
如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com