
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.
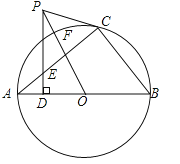
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中有点B(-2,0)和y轴上的动点A(0,a),其中a>0,以点A为直角顶点在第二象限内作等腰直角三角形ABC,设点C的坐标为(c,d).
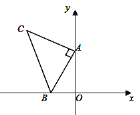
(1)当a=4时,则点C的坐标为( , );
(2)动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
(3)当a=4时,在坐标平面内是否存在点P(不与点C重合),使△PAB与△ABC全等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:a+![]() ,其中a=1010.
,其中a=1010.
如图是小亮和小芳的解答过程.
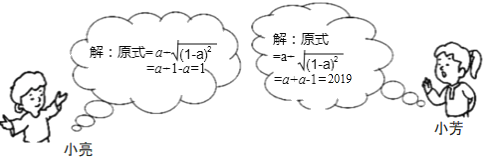
(1) 的解法是错误的,错误的原因在于未能正确地运用二次根式的性质:![]() = (a<0);
= (a<0);
(2)先化简,再求值:x+2![]() ,其中x=﹣2019.
,其中x=﹣2019.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“文明礼仪”在人们长期生活和交往中逐渐形成,并以风俗、习惯等方式固定下来的.我们作为具有五千年文明史的“礼仪之邦”,更应该用文明的行为举止, 合理的礼仪来待人接物.为促进学生弘扬民族文化、展示民族精神,某学校开展“文明礼仪”演讲比赛,八年级(1)班,八年级(2)班各派出 5 名选手参加比赛,成绩如图所示.
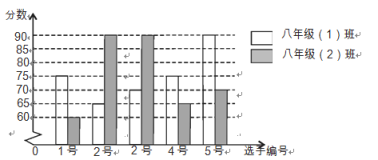
(1)根据图,完成表格:
平均数(分) | 中位数(分) | 极差(分) | 方差 | |
八年级(1)班 | 75 |
| 25 |
|
八年级(2)班 | 75 | 70 |
| 160 |
(2)结合两班选手成绩的平均分和方差,分析两个班级参加比赛选手的成绩;
(3)如果在每班参加比赛的选手中分别选出3人参加决赛,从平均分看,你认为哪个班的实力更强一些? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
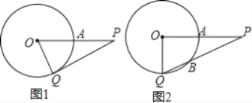
【题目】已知P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )
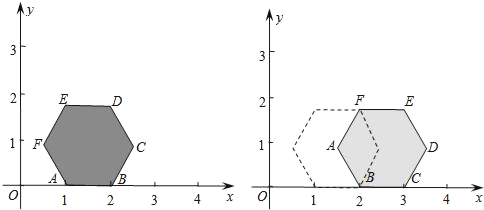
A. (2017,0) B. (2017,![]() )
)
C. (2018,![]() ) D. (2018,0)
) D. (2018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的各边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG.

(1)求证:△BDE≌△BAC;
(2)求证:四边形ADEG是平行四边形.
(3)直接回答下面两个问题,不必证明:
①当△ABC满足条件_____________________时,四边形ADEG是矩形.
②当△ABC满足条件_____________________时,四边形ADEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识
的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,
并将检查结果绘制成下面两个统计图.
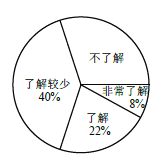
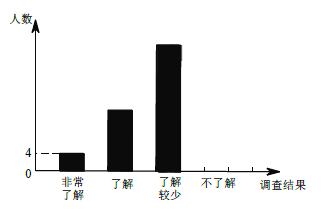
(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人.
(2)“非常了解”的4 人有![]() 两名男生,
两名男生,![]() 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象过A(1,1)和B(2,﹣1)
(1)求一次函数y=kx+b的表达式;
(2)求直线y=kx+b与坐标轴围成的三角形的面积;
(3)将一次函数y=kx+b的图象沿y轴向下平移3个单位,则平移后的函数表达式为 ,再向右平移1个单位,则平移后的函数表达式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com