
【题目】已知一次函数y=kx+b的图象过A(1,1)和B(2,﹣1)
(1)求一次函数y=kx+b的表达式;
(2)求直线y=kx+b与坐标轴围成的三角形的面积;
(3)将一次函数y=kx+b的图象沿y轴向下平移3个单位,则平移后的函数表达式为 ,再向右平移1个单位,则平移后的函数表达式为 .
【答案】(1)y=﹣2x+3;(2)![]() ;(3)y=﹣2x,y=﹣2x+2
;(3)y=﹣2x,y=﹣2x+2
【解析】
(1)把A、B两点代入可求得k、b的值,可得到一次函数的表达式;
(2)分别令y=0、x=0可求得直线与两坐标轴的两交点坐标,可求得所围成的三角形的面积;
(3)根据上加下减,左加右减的法则可得到平移后的函数表达式.
解:(1)∵一次函数y=kx+b的图象过A(1,1)和B(2,﹣1),
∴![]() ,解得
,解得![]() ,
,
∴一次函数为y=﹣2x+3;
(2)在y=﹣2x+3中,分别令x=0、y=0,
求得一次函数与两坐标轴的交点坐标分别为(0,3)、(![]() ,0),
,0),
∴直线与两坐标轴围成的三角形的面积为:S=![]() ×3×
×3×![]() =
=![]() ;
;
(3)将一次函数y=﹣2x+3的图象沿y轴向下平移3个单位,则平移后的函数表达式为y=﹣2x,再向右平移1个单位,则平移后的函数表达式为y=﹣2(x﹣1),即y=﹣2x+2
故答案为:y=﹣2x,y=﹣2x+2.


科目:初中数学 来源: 题型:
【题目】青岛某高中允许高三学生从寄宿、走读两种方式中选择一种就读,今年新高三学生总人数与去年相比增加了6%,其中选择寄宿的学生增加了20%,选择走读的学生减少了15%,若去年高三学生的总数为500人,求今年新高三学生选择寄宿和走读的人数分别是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FOED=ODEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
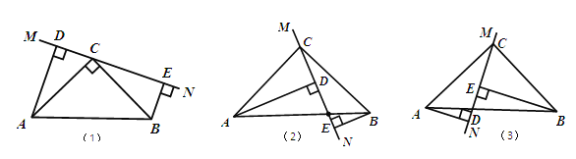
(1)当直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图(3)的位置时,试问:DE,AD,BE有怎样的等量关系?请写出这个等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,∠A=∠EDF,再添加一个条件,可使△ABC ≌ △DEF,下列条件不符合的是
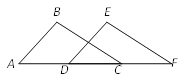
A.∠B=∠EB.BC∥EFC.AD=CFD.AD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
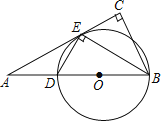
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,傅家堰中学新修了一个运动场,运动场的两端为半圆形,中间区域为足球场,外面铺设有塑胶环形跑道,四条跑道的宽均为1米.
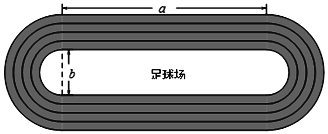
(1)用含a、b的代数式表示塑胶环形跑道的总面积;
(2)若a=60米,b=20米,每铺1平方米塑胶需120元,求四条跑道铺设塑胶共花费多少元?(π=3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com