
����Ŀ������ABC�У���ACB��90����AC��BC��ֱ��MN������C����AD��MN�ڵ�D��BE��MN�ڵ�E��
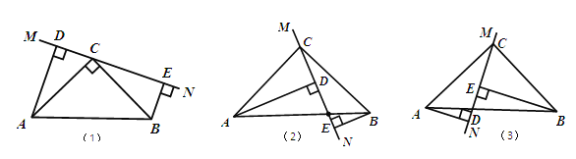
��1����ֱ��MN�Ƶ�C��ת��ͼ��1����λ��ʱ����֤��DE��AD��BE��
��2����ֱ��MN�Ƶ�C��ת��ͼ��2����λ��ʱ����֤��DE��AD��BE��
��3����ֱ��MN�Ƶ�C��ת��ͼ��3����λ��ʱ�����ʣ�DE��AD��BE�������ĵ�����ϵ����д�����������ϵ��������֤����
���𰸡���1������������2������������3��DE��BE��AD��֤��������
��������
��1�����ô�ֱ�Ķ���á�ADC=��CEB=90�㣬����ݻ���á�DAC+��ACD=90�㣬�ٸ��ݵȽǵ������ȵõ���DAC=��BCE��Ȼ����ݡ�AAS�����жϡ�ADC�ա�CEB������CD=BE��AD=CE�������õ��������õ�DE=AD+BE��
��2���루1��֤�����ƿ�֤����DAC=��BCE�����Ƴ���ADC�ա�CEB���õ�AD=CE��CD=BE���Ӷ���DE=CE-CD=AD-BE��
��3���루1��֤�����ƿ�֤����DAC=��BCE�����Ƴ���ADC�ա�CEB���õ�AD=CE��CD=BE��������DE=CD-CE=BE-AD��
��1��֤������AD��MN,BE��MN
���ADC����CEB��90��
���DAC����DCA��90��
�ߡ�ACB��90��
���ECB����DCA��90��
���DAC����ECB
����ACD����CBE��
��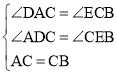
���ACD�ա�CBE(AAS)
��CE��AD, CD��BE
��DE��CE��CD
��DE��AD��BE
��2��֤�����루1��һ����֤����ADC�ա�CEB��
��CD=BE��AD=CE��
��DE=CE-CD=AD-BE��
��3��DE��BE��AD��֤�����£�
֤����֤������AD��MN,BE��MN
���ADC����CEB��90��
���DAC����DCA��90��
�ߡ�ACB��90��
���ECB����DCA��90��
���DAC����ECB
����ACD����CBE��
��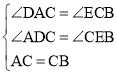
���ACD�ա�CBE(AAS)
��CE��AD, CD��BE
��DE=CD-CE= BE-AD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������վ�ڲ���ݵ�չ������ʱ����֪��վ�ںδ���������������ͼ����ǽ���ϵ�չƷ��ߵ�P�����2.5�ף���͵�Q�����2�ף������ߵ��۾�F�����1.6�ף����ӽ���PEQ���ʱ��վ�ڴ˴����������룬���ʱE��ǽ�ڵľ���Ϊ�� ���ף�

A. 1 B. 0.6 C. 0.5 D. 0.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���е�һ����3000Ԫ����ij�ָɹ����ۣ��ڶ����ֵ���9000Ԫ�������ָɹ������ڶ��εĽ��۱ȵ�һ�εĽ��������20%�������ɹ������ǵ�һ�ε�2������300ǧ�ˣ���������Ȱ�ÿǧ��9Ԫ�ļ۸���ۣ����ָɹ����ۺ�����600ǧ�˰�ԭ�ۼ۵�7�����꣬���������������ָɹ���ӯ��________Ԫ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
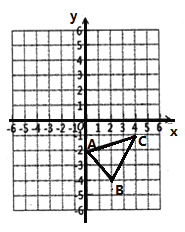
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�
��1������![]() ����
����![]() ��ԳƵ�
��ԳƵ�![]() ����д��
����д��![]() ������������ꣻ
������������ꣻ
��2�������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
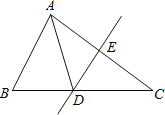
����Ŀ����ͼ������ABC�У�AC�Ĵ�ֱƽ���߽�BC��D����AC��E��AE��3cm�� ��ABD���ܳ�Ϊ13cm����ô��ABC���ܳ�Ϊ_______________cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������⣩��ͼ1����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��������һ�㣬����
��������һ�㣬����![]() ��
��![]() ��
��![]() ������ֱ�Ϊ��
������ֱ�Ϊ��![]() ����
����![]() ��
��
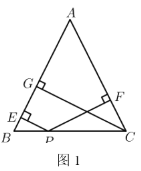
��1����![]() ��
��![]() ����
����![]() �������______��
�������______��![]() ______��
______��
��2�������߶�![]() ��
��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
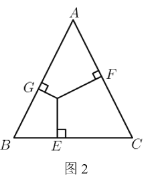
��3������ʽ̽������ͼ2����![]() �У���
����![]() ����
����![]() ��
��![]() ������һ�㣬��
������һ�㣬��![]() ��
��![]() ��
��![]() ������ֱ�Ϊ��
������ֱ�Ϊ��![]() ����
����![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
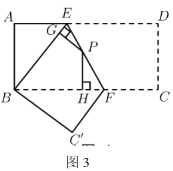
��4������չ���죩��ͼ3����������![]() ��
��![]() �۵���ʹ��
�۵���ʹ��![]() ���ڵ�
���ڵ�![]() �ϣ���
�ϣ���![]() ���ڵ�
���ڵ�![]() ������
������![]() Ϊ�ۺ�
Ϊ�ۺ�![]() �ϵ�����һ�㣬����
�ϵ�����һ�㣬����![]() ��
��![]() ��
��![]() ������ֱ�Ϊ��
������ֱ�Ϊ��![]() ����
����![]() ����
����![]() ��
��![]() ��ֱ��д��
��ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y��kx+b��ͼ���A(1��1)��B(2����1)
��1����һ�κ���y��kx+b�ı���ʽ��
��2����ֱ��y��kx+b��������Χ�ɵ������ε������
��3����һ�κ���y��kx+b��ͼ����y������ƽ��3����λ����ƽ�ƺ�ĺ�������ʽΪ�� ����������ƽ��1����λ����ƽ�ƺ�ĺ�������ʽΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
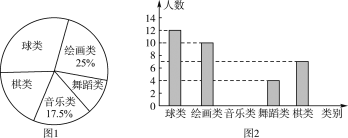
����Ŀ��Ϊ�˽�ijУ��ʵ�¿θľ������������Ը�У���꼶�����ͬѧ�μӿ��������Ϊ����������μӡ����ࡱ���滭�ࡱ���赸�ࡱ�������ࡱ�����ࡱ���������е���ͳ�ƣ�����������ͼ��ʾ��ͳ��ͼ��
(1)�μ���������ѧ������Ϊ____�ˣ��μ������������İٷֱ�Ϊ____��
(2)�������ͳ��ͼ����������
(3)����Уѧ����600�ˣ���ô�μ������Ĵ�Լ�ж����ˣ�
(4)�ð�μ��赸����4λͬѧ�У���1λ����(��E��ʾ)��3λŮ��(�ֱ���F��G��H��ʾ)����������ѡȡ����ͬѧ�����飬�����б�����״ͼ�ķ�����ǡ��ѡ��һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��ֱ��AB��DE֮���һ�㣬��ACD=90�㣬����������ʹ��AB��DE���ǣ�����
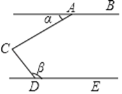
A. ����+����=180�� B. ����������=90�� C. ����=3���� D. ����+����=90��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com