
【题目】如图,以△ABC的各边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG.

(1)求证:△BDE≌△BAC;
(2)求证:四边形ADEG是平行四边形.
(3)直接回答下面两个问题,不必证明:
①当△ABC满足条件_____________________时,四边形ADEG是矩形.
②当△ABC满足条件_____________________时,四边形ADEG是正方形?
【答案】(1)见解析;(2)见解析;(3)①∠BAC=135°;②∠BAC=135°且AC=![]()
【解析】
(1)根据全等三角形的判定定理SAS证得△BDE≌△BAC;
(2)由△BDE≌△BAC,可得全等三角形的对应边DE=AG.然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG=180°,易证ED∥GA;最后由“一组对边平行且相等”的判定定理证得结论;
(3)①根据“矩形的内角都是直角”易证∠DAG=90°.然后由周角的定义求得∠BAC=135°;
②由“正方形的内角都是直角,四条边都相等”易证∠DAG=90°,且AG=AD.由正方形ABDI和正方形ACHG的性质证得:AC![]() AB.
AB.
(1)∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°,∴∠ABC=∠EBD(同为∠EBA的余角).
在△BDE和△BAC中,∵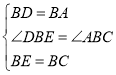 ,∴△BDE≌△BAC(SAS);
,∴△BDE≌△BAC(SAS);
(2)∵△BDE≌△BAC,∴DE=AC=AG,∠BAC=∠BDE.
∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.
∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC,∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°,∴DE∥AG,∴四边形ADEG是平行四边形(一组对边平行且相等).
(3)①当四边形ADEG是矩形时,∠DAG=90°.
则∠BAC=360°﹣∠BAD﹣∠DAG﹣∠GAC=360°﹣45°﹣90°﹣90°=135°,即当∠BAC=135°时,平行四边形ADEG是矩形;
②当四边形ADEG是正方形时,∠DAG=90°,且AG=AD.
由①知,当∠DAG=90°时,∠BAC=135°.
∵四边形ABDI是正方形,∴AD![]() AB.
AB.
又∵四边形ACHG是正方形,∴AC=AG,∴AC![]() AB,∴当∠BAC=135°且AC
AB,∴当∠BAC=135°且AC![]() AB时,四边形ADEG是正方形.
AB时,四边形ADEG是正方形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
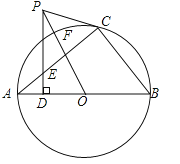
【题目】如图钢架中,∠A=15°,现焊上与AP1等长的钢条P1P2,P2P3…来加固钢架,若最后一根钢条与射线AB的焊接点P到A点的距离为4+2![]() ,则所有钢条的总长为( )
,则所有钢条的总长为( )
A.16B.15C.12D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
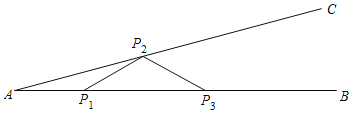
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折叠,使点B落在CA边上的B′处,展开后,再沿BE折叠,使点C落在BA边上的C′处,CD与BE交于点F.
(1)求AC′的长度;
(2)求CE的长度;
(3)比较四边形EC′DF与△BCF面积的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac.其中正确的有( )
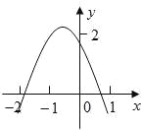
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,“复兴一号“水稻的实验田是边长为m米的正方形去掉一个边长为n米(m>n)正方形蓄水池后余下的部分,“复兴二号“水稻的试验田是边长为(m-n)米的正方形,两块试验田的水稻都收获了a千克.
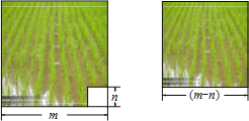
(1)哪种水稻的单位面积产量高?为什么?
(2)高的单位面积产量比低的单位面积产量高多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com