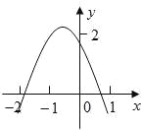
【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），且与x轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：①4a﹣2b+c＜0；②2a﹣b＜0；③a+c＜1；④b2+8a＞4ac.其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
解：①根据图象知，当x=-2时，y＜0，即4a-2b+c＜0；故本选项正确；
②∵该函数图象的开口向下，
∴a＜0，
又∵对称轴-1＜x=-
＜0，
∴2a-b＜0，故本选项正确；
③已知抛物线经过（-1,2），即a-b+c=2（1），
由图知：当x=1时，y＜0，即a+b+c＜0（2），
联立（1）（2），得：a+c＜1，故本选项正确；
④∵y=
＞2，a＜0，
∴4ac-b2＜8a，即b2+8a＞4ac，故本选项正确；
综上所述，正确的结论有4个.
故选：D．
科目：初中数学 来源： 题型：
【题目】先化简，再求值：a+
，其中a＝1010．
如图是小亮和小芳的解答过程．
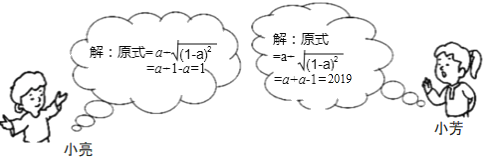
（1） 的解法是错误的，错误的原因在于未能正确地运用二次根式的性质：
＝ （a＜0）；
（2）先化简，再求值：x+2
，其中x＝﹣2019．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以△ABC的各边，在边BC的同侧分别作三个正方形ABDI，BCFE，ACHG．
（1）求证：△BDE≌△BAC；
（2）求证：四边形ADEG是平行四边形．
（3）直接回答下面两个问题，不必证明：
①当△ABC满足条件_____________________时，四边形ADEG是矩形．
②当△ABC满足条件_____________________时，四边形ADEG是正方形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着经济的快速发展，环境问题越来越受到人们的关注，某校学生会为了解节能减排、垃圾分类知识
的普及情况，随机调查了部分学生，调查结果分为“非常了解”“了解”“了解较少”“不了解”四类，
并将检查结果绘制成下面两个统计图．
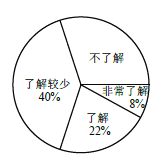
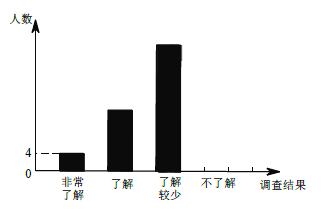
（1）本次调查的学生共有__________人，估计该校1200 名学生中“不了解”的人数是__________人．
（2）“非常了解”的4 人有
两名男生，
两名女生，若从中随机抽取两人向全校做环保交流，请利用画树状图或列表的方法，求恰好抽到一男一女的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
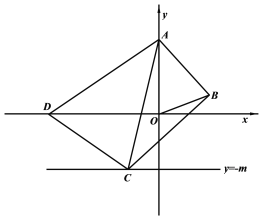
【题目】已知：如图，在平面直角坐标系中，O为坐标原点，△OAB的顶点A、B的坐标分别是A（0，5），B（3，1），过点B画BC⊥AB交直线
于点C，连结AC，以点A为圆心，AC为半径画弧交x轴负半轴于点D，连结AD、CD．
（1）求证：△ABC≌△AOD．
（2）设△ACD的面积为
，求关于
的函数关系式．
（3）若四边形ABCD恰有一组对边平行，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD⊥BC于D，BE⊥AC于F，BE交AD于F，BF＝AC，
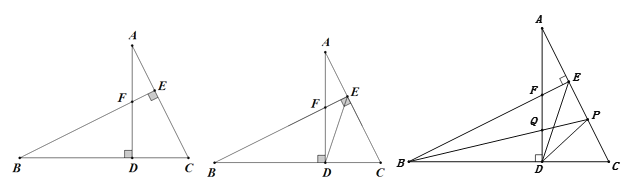
（1）求证：FD＝CD；
（2）连DE，求证：ED平分∠BEC；
（3）在（2）条件下，点P在AC上，连BP、DP，BP交AD于Q， BP平分∠EBC，∠BPD＝
∠BFD，△APQ的面积为4，求线段PD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
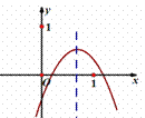
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，则在下列代数式:①ac；②a+b+c；③4a-2b+c；④2a+b；⑤b2-4ac中，值大于0的序号为______________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数y＝kx+b的图象过A(1，1)和B(2，﹣1)
（1）求一次函数y＝kx+b的表达式；
（2）求直线y＝kx+b与坐标轴围成的三角形的面积；
（3）将一次函数y＝kx+b的图象沿y轴向下平移3个单位，则平移后的函数表达式为 ，再向右平移1个单位，则平移后的函数表达式为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+2ax+3a2+3（其中x是自变量），当x≥2时，y随x的增大而增大，且2≤x≤1时，y的最大值为9，则a的值为
A. 1或2 B. 
或
C. D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com